基本介紹
- 中文名:預測函式控制
- 外文名:Predictive function control
- 簡稱:PFC
- 提出者:Richalet 和 Kuntze 等
- 提出時間:80年代中後期提出
- 優點:算法簡單、計算量小、跟蹤快速等
背景
簡介
基本原理
基函式與模型輸出











參考軌跡
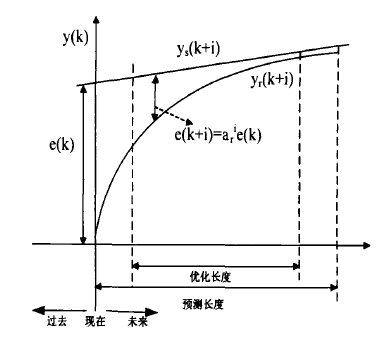






預測誤差與反饋校正





滾動最佳化







基本結構
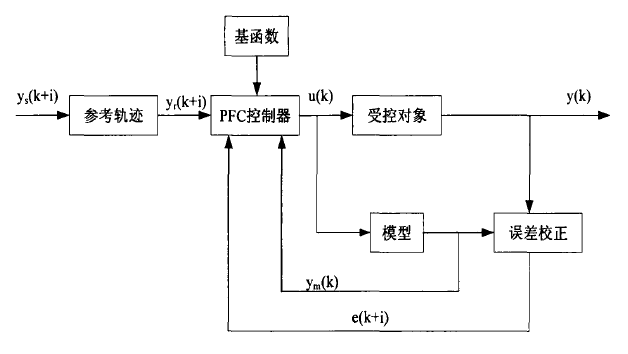
































預測函式控制 (Predictive function control,簡稱PFC)是第三代模型預測控制算法,它是由 Richalet 和 Kuntze 等人在 80年代中後期提出,並成功地套用於工業機器人的快速高精度控...
常用的預測控制算法有:(1)動態矩陣控制(Dynamic Matrix Control, DMC)(2)模型算法控制(Model Algorithm Control, MAC)(3)廣義預測控制(Generalized Predictive Control, GPC)(4)預測函式控制(Predictive Functional Control, PFC)預測控制基本原理 1978年, J.Richalet等就提出了預測控制算法的三要素:...
預測控制是一種基於模型的控制算法,這一模型稱為預測模型。預測模型的功能是根據對象的歷史信息和未來輸入預測其未來輸出。這裡只強調模型的功能而不強調其結構形式。因此,狀態方程、傳遞函式這類傳統的模型都可以作為預測模型。對於線性穩定對象,甚至階躍回響、脈衝回響這類非參數模型,也可直接作為預測模型使用。此外...
與前一個預測 PI 控制器相比較而言,該控制器引入可調參數 ,其主要作用是改變系統回響的速度。若 =1 時,則系統開環和閉環具有相同的時間常數;若 >1 時,則系統閉環回響速度慢於開環回響速度;若 結構形式 圖1為單位負反饋控制系統。Gc(s)是控制器,Gp(s)是被控對象的傳遞函式,由圖1可得出閉環...
預測控制是一種基於模型的控制算法,該模型被稱為預測模型。對於預測控制而言,只注重模型功能,而不是模型的形式。預測模型是基於對象的歷史信息和輸入,預測其未來的輸出。從方法論的角度來看,只要信息的收集具有預測功能,無論什麼樣的表現,可以作為預測模型。這樣的狀態方程、模型傳遞函式都可以用來作為一個傳統的...
6. 1 預測函式控制 6. 1. 1 預測函式控制的基本原理 6. 1. 2 典型環節的PFC算法 6. 1. 3 預測函式控制的內模結構 6. 2 多速率採樣預測控制 6. 2. 1 多速率採樣系統建模 6. 2. 2 多速率採樣預測控制算法 6. 2. 3 多速率廣義預測控制 6. 3 多模型切換預測控制 6. 3. 1 線性定常系統的多...
MAC控制是一種基於對象脈衝回響的預測控制算法,它適用於漸進穩定的線性對象。為此,模組還增加了系統判穩的功能,對於不穩定的系統,該模組會發出錯誤警告,直到輸入的系統為穩定時為止。(2)系統回響模組:系統回響模組的功能是構建系統的脈衝傳遞函式Hₘ(q)。對於高階系統(大於2階系統),取其主導極點,可以降為2...
6.4.1 模糊C-均值聚類函式 (247)6.4.2 模糊減法聚類函式 (248)6.4.3 基於減法聚類的模糊推理系統建模函式 (250)6.4.4 模糊C-均值和減法聚類的圖形用戶界面 (252)小結 (254)思考練習題 (254)第三篇 模型預測控制及其MATLAB實現 第7章 模型預測控制理論 (255)7.1 動態矩陣控制理論 (255...
為了解決最優控制問題,必須建立描述受控運動過程的運動方程,給出控制變數的允許取值範圍,指定運動過程的初始狀態和目標狀態,並且規定一個評價運動過程品質優劣的性能指標。通常,性能指標的好壞取決於所選擇的控制函式和相應的運動狀態。系統的運動狀態受到運動方程的約束,而控制函式只能在允許的範圍內選取。因此,從...
以被控量x在tₖ時刻的採樣值x(k)為基礎,利用離散數學模型,通過對變換器所有可能的開關狀態進行預測,最終獲得多目標函式最優解對應的開關狀態並將其作用於變換器。這種算法本質上僅考慮換流器被控量在一個控制周期內最優狀態,即能夠實現短期最優控制效果,而對於建立在上述最優開關狀態下的被控量能否在接...
面向間歇過程的高效2D預測函式控制算法、面向間歇過程的二維遞歸最小二乘辨識算法、基於MVU濾波器的無偏模型預測控制算、基於收斂深度控制的嵌入式預測控制算法等研究成果,並在注塑機工業平台上加以套用驗證。通過本項目的研究,豐富了現有間歇過程的控制理論和方法,為實際套用的開展提供方法及技術支撐。
實用的預測控制方法有動態矩陣控制(DMC),模型算法控制(MAC),廣義預測控制(GPC),模型預測啟發控制(MPHC)以及預測函式控制(PFC)等。這些方法具有以下特徵:⑴以計算機為實現手段,採取線上實現方式;⑵建模方便,不需深入了解過程的內部機理,對模型精度要求不高;⑶採用滾動最佳化策略,線上反覆進行最佳化計算,使...
隨著工業生產過程對最佳化技術日益增長的技術需求,經濟性預測控制研究已經迅速發展為預測控制的一個新的重要分支,並且成為當前國際上預測控制研究的前沿和難點。本項目主要研究構造準經濟指標,設計預測控制算法,將經濟性預測控制通過傳統的跟蹤性預測控制框架進行實現的問題。通過引入HESSIAN矩陣、基於耗散性的終端懲罰函式、...
6.4.1 模糊C-均值聚類函式 (281)6.4.2 模糊減法聚類函式 (282)6.4.3 基於減法聚類的模糊推理系統建模函式 (284)6.4.4 模糊C-均值和減法聚類的圖形用戶界面 (285)小結 (288)思考練習題 (288)第三篇 模型預測控制及其MATLAB實現 第7章 模型預測控制理論 (289)7.1 動...
線性狀態反饋魯棒預測控制 這種算法根據採樣時刻的狀態反饋求解線性控制律,並作用到系統中,使系統滿足輸入約束和狀態約束,並使目標函式在無限時域內單調遞減,保證穩定性,這樣就可以把線上最佳化問題用線性矩陣不等式(LMI)方法進行計算。如果在初始採樣時刻的線上最佳化問題可以用LMI求解,那么在以後的採樣時刻進行滾動最佳化都...
(2)基於神經網路控制器的神經網路預測控制。這種方法基於兩個神經網路,一個是建模網路,用於過程的動態建模以獲取對過程的預測信號;另一個是控制網路,它按照與預測控制目標函式相應的驅動信號來調整整個網路的權值,以獲取對預測控制律函式的逼近。神經網路預測控制結構 結構 神經網路預測控制系統結構如圖3所示。圖中:...
6.4.1 模糊C-均值聚類函式 (280)6.4.2 模糊減法聚類函式 (281)6.4.3 基於減法聚類的模糊推理系統建模函式 (283)6.4.4 模糊C-均值和減法聚類的圖形用戶界面 (284)小結 (287)思考練習題 (287)第三篇 模型預測控制及其MATLAB實現 第7章 模型預測控制理論 (288)7.1 動態矩陣控制理論 (288...
5.6 多變數單值預估控制 204 5.6.1 多變數單值預估控制算法 204 5.6.2 大滯後系統的多變數單值廣義預測控制 206 5.7 廣義預測-PID串級控制 209 5.7.1 GPC-PID串級控制的結構與特點 209 5.7.2 仿真試驗 210 5.7.3 GPC-PID 串級控制的實施方案 213 5.8 基於差分方程的單變數預測函式控制 214 5....
(3) 跟蹤控制,亦稱隨動控制。輸入給系統的參照量是隨某個變數(先行量) 而變化的量 (跟隨量),即參照量是關於某個非時間變數的已知函式,其控制是使系統的輸出量跟隨系統的輸入量,從而跟隨先行量而變化。市場調節是典型的跟蹤控制,價格跟隨供需變化,企業跟隨價格生產(4) 超前控制,亦稱預測控制。輸入給系統的...
VSPC在機組協調控制中的套用 變結構控制是一種普遍適用的控制系統綜合方法,它利用切換函式將控制系統的設計轉化為求解控制量,因而系統設計比較簡單。與傳統的預測控制方法相比,該算法具有設計簡單、易於實現的優點。採用以上變結構預測控制算法,可以套用協調的控制策略。在控制結構上,新協調方案保留常規鍋爐主控方案中...
