項鍊問題(problem of necklace)是一種圓排列問題,設由n個珠子串成一條項鍊,每個珠子可有r種不同的顏色,試問共有多少種不同花色的項鍊?(其中,兩個項鍊認為是同一花色是指將一個項鍊朝一個方向旋轉某個角度之後,便與另一個項鍊完全一樣)。這個問題稱為項鍊問題。
基本介紹
- 中文名:項鍊問題
- 外文名:problem of necklace
- 所屬學科:數學
- 所屬問題:組合計數問題
- 簡介:可理解為第二種雙繞向圓排列
基本介紹

兩類項鍊問題的解















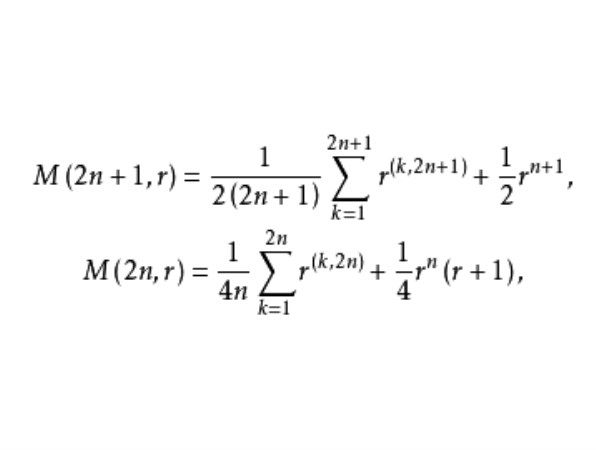
項鍊問題(problem of necklace)是一種圓排列問題,設由n個珠子串成一條項鍊,每個珠子可有r種不同的顏色,試問共有多少種不同花色的項鍊?(其中,兩個項鍊認為是同一花色是指將一個項鍊朝一個方向旋轉某個角度之後,便與另一個項鍊完全一樣)。這個問題稱為項鍊問題。
















項鍊問題(problem of necklace)是一種圓排列問題,設由n個珠子串成一條項鍊,每個珠子可有r種不同的顏色,試問共有多少種不同花色的項鍊?(其中,兩個項鍊認為是同一花色是指將一個項鍊朝一個方向旋轉某個角度之...
項鍊排序是組合數學中一個很常見的問題,可以在圓排列的基礎上求解。·圓周排列:從n箇中取r個的圓排列的排列數為 P(n,r)/r , 2≤r≤n ·項鍊排列:正面向上和反面向上兩種方式放置各個數是同一個排列。因此,從n箇中取r個的...
工藝因素。一些低端品牌首飾製造工藝不過關,如果焊點工藝差的話,出現虛焊等問題,也容易導致項鍊斷裂。水晶項鍊 水晶項鍊作為一種飾品,以水晶的透明、夢幻、閃亮的材質與效果征服了無數女子的心。水晶項鍊的分類:一般分為紫水晶項鍊、黃...
項鍊:金銀、珠寶製成的掛在頸上的鏈條形狀的首飾。項鍊是由一根長鏈索穿以各色珍珠玉石後,纏繞於項,也有配以搭扣、以方便摘取的短鏈。一般在項鍊下方還懸有精美的墜飾,以達到畫龍點睛的效果。相關問題 Q:水晶項鍊如果沒有搭扣,...
但只要保持清潔乾淨,不受高溫和強力碰撞,應該不會有問題的。藏品介紹 綠松石項鍊,該藏品綠松石琢成不規則小珠,共有171粒,中穿孔,串穿製成。原穿連方式不明。項鍊介紹 綠松石項鍊,戰國,長2cm,寬1.3cm,厚0.5cm。綠松石均...
2014年11月,哈爾濱南崗區一地下商場,一戴眼鏡的長髮女子因長時間梳理、補妝,引起他人不滿。在她人和其理論,並引發拉扯過程中,該化妝女大叫:”我的項鍊兩千多……“。隨後,成為網路熱點。事件經過 2014年11月23日下午5時許,...
(1)課文學完了,你還有問題嗎?學生自由提問。(2)小結:海邊有藍藍的海,金黃的沙灘,淘氣、熱情的浪花,熱愛生活的小娃娃。我們感受到了大海美,沙灘美,浪花美,小娃娃串的項鍊美,她玩得美,其實是我們的生活美!(3)有感情...
現代彝族銀項鍊 現代彝族銀項鍊是重慶中國三峽博物館收藏的金銀器。
方形G純銀項鍊是古馳品牌旗下的一款產品。產品介紹 點綴精美的阿拉伯刻花圖案,純銀吊墜上勾勒出鏤空圖案,懸垂在刻花環鏈上。產品參數 做舊效果純銀 方形G鏤空吊墜 夾扣 吊墜:1.5厘米(寬)x 1.5厘米(高)長80厘米,可調節至90...
紅色項鍊合適嗎?紅色項鍊 合適嗎?是きたむらとおる創作的漫畫。漫畫內容 紅色項鍊 合適嗎?漫畫 ,Love Live的同人本。
COCO CRUSH系列項鍊 COCO CRUSH系列項鍊是香奈兒品牌旗下的一款產品。
美杜莎項鍊是范思哲品牌旗下的一款產品。產品簡介 此款粗鏈式項鍊採用標誌性的Versace設計,飾有傳統美杜莎徽章。所有Versace珠寶產品均不含鉛和鎳。所有材質均為低敏感性。產品參數 鏈式項鍊 美杜莎徽章 掛鈎閉合 金屬:黃銅 拋光:Versace...
Nuri鸚鵡項鍊是寶詩龍旗下的一款產品。 設計理念 “NURI”在印度尼西亞語中意指鸚鵡,白鸚鵡是一種調皮又充滿靈性的動物。其羽毛華美而豐盈,象徵著構成生命的陽光、水和火等元素。因此,對於此款珠寶的女性佩戴者而言,NURI鸚鵡是美與...
虎頭銀項鍊 虎頭銀項鍊是古馳品牌旗下的一款產品。產品介紹 純銀項鍊,配以復古深色塗層和虎頭吊墜。產品參數 純銀,配以復古塗層 龍蝦扣 60厘米長 義大利創作
Identity 項鍊 Identity 項鍊是亞歷山大麥昆品牌旗下的一款產品。產品介紹 古銀色項鍊,搭配 Alexander McQueen 標牌與骷髏墜飾。古銀色處理黃銅硬體。
互扣式雙G吊墜項鍊是古馳品牌旗下的一款產品。產品簡介 自問世以來,互扣式雙G一直是品牌的標誌性設計元素。這款純銀項鍊巧妙結合了三個吊墜設計,生動演繹三種別致的品牌符號。產品參數 純銀 互扣式雙G細節 搭扣 60厘米長 ...
通過醞釀,最近的記憶和已有的記憶被整合在一起,弱化了心理定勢的效應,並容易激活比較遙遠的思維線索,因而容易重構出新的事物,產生對問題的新看法,使問題得以順利解決。有人用實驗說明了這種效應。給被試提出經濟項鍊問題:有四條小...
他本人在創作《蒙娜麗莎》時,認真地研究了主人公的心理,做了各種精確的數學計算,來確定人物的比例結構,以及半身人像與背景間關係的構圖問題。當我們欣賞他的《抱銀貂的女人》中脖頸上懸掛的黑色珍珠項鍊時,我們注意的是項鍊與女人相互...
首飾病,是指佩戴金屬首飾引發的接觸性皮炎,通常是指有過敏體質的人接觸到一些金屬如鎳、鉻、鈦等引起的過敏反應。常見的首飾如戒指、耳環、項鍊、以及手鍊、手錶、眼鏡框、衣褲扣、含有金屬線的圍巾等都含有鉻和鎳,都會使直接接觸的...
首飾,原指戴於男士頭上的帽子,當前廣泛指以貴重金屬、寶石等加工而成的雀釵、耳環、項鍊、戒指、手鐲等。首飾一般用以裝飾人體,也具有表現社會地位、顯示財富及身份的意義。基本解釋 1. [ouch;jewelry] 原指男女戴在頭上的裝飾品,...
項墜,讀音是xiàng zhuì,漢語詞語,意思為項鍊上下垂的首飾品。解釋 項鍊上下垂的首飾品。出處 《傳記文學》1990年第6期:“伯華低頭一看,盒子裡金絲絨上放著一根精工打制的金項鍊,中間是精巧的‘心’字金項墜,心字里嵌著伯華和...
無焊千足金徹底解決了使用焊料的問題,消費者購買可以以無焊作為購買依據。含金屬銥 2013年3月15日,3·15晚會曝光,在一些商場黃金專櫃出售的千足金,含量並不達標。在深圳的水貝珠寶城,記者見證了首飾加工行業將黃金中加入價格低廉的...
