手鐲問題(problem of bracelet)是一種圓排列問題,用r種不同顏色的珠子穿成手鐲,求所有不同的手鐲數,這個問題稱為手鐲問題。手鐲問題應解釋為第一種單繞向圓排列。
基本介紹
- 中文名:手鐲問題
- 外文名:problem of bracelet
- 所屬學科:數學
- 所屬問題:組合計數問題
基本介紹



相關介紹

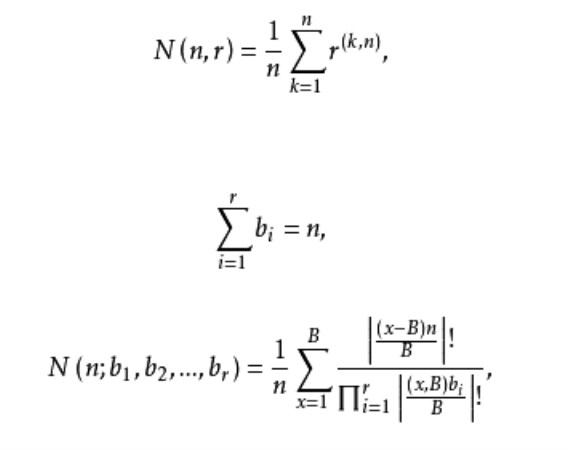
手鐲問題(problem of bracelet)是一種圓排列問題,用r種不同顏色的珠子穿成手鐲,求所有不同的手鐲數,這個問題稱為手鐲問題。手鐲問題應解釋為第一種單繞向圓排列。




手鐲問題(problem of bracelet)是一種圓排列問題,用r種不同顏色的珠子穿成手鐲,求所有不同的手鐲數,這個問題稱為手鐲問題。手鐲問題應解釋為第一種單繞向圓排列...
手鐲(bracelet; bangle ),是用金、銀、玉等制的戴在手腕上的環形裝飾品。按結構,一般可分為兩種:一是封閉形圓環,以玉石材料為多;二是有連線埠或數個鏈片,以...
手鐲,亦稱“釧”、“手環”、“臂環”等,是一種戴在手腕部位的環形裝飾品。其質料除了金、銀、玉之外,尚有用植物藤製成者。手鐲由來已久,起源於母系社會向父...
和田玉手鐲:和田玉是中華民族的瑰寶,是中國國石。2003年10月曆經幾年的中國“國玉”評選工作結束,和田玉獲得“美玉”稱號,被中國寶玉石協會正式命名為“中國國石...
《中國傳統首飾·手鐲戒指耳飾》中國傳統首飾豐富多彩、美不勝收,且蘊涵了深厚的文化內涵和民族精神,具有較高的實物價值和文史價值。筆者憑藉三十餘年的研究心得和...
項鍊問題(problem of necklace)是一種圓排列問題,設由n個珠子串成一條項鍊,每個珠子可有r種不同的顏色,試問共有多少種不同花色的項鍊?(其中,兩個項鍊認為是...
包裝完成後由品檢部檢查數量,如沒問題則進行封箱並送交倉庫等待發貨矽膠...等特點和 柔軟、不開裂、使用壽命長、不刺激皮膚等優點 ,矽膠手鐲是真正的綠色...
若是翡翠手鐲在自己沒有保護好的情況下破碎了,由於冰糯種飄花玉鐲能通人性,因此在翡翠手鐲破損手,將其埋在土中,好好安置,便不會出現任何問題。冰...
這種號稱能量“平衡手環”能不斷地提供外來的磁力能量以解決地球磁場耗減的問題...baldassi也戴這個平衡手鐲。 其他運動員也戴這款手鐲。最著名的是巴里切羅(f1),...
