Herman,Rothery、Gazis等人,假定跟車模型中獲得性因子與後車的速度成m次冪的正比例關係,與前後車之間的相對距離成l次冪的反比例關係,我們推導出一個非線性的跟車模型,後來有人稱它為“L&M模型”。對該方程積分可以產生各種想要的流量/密度方程。
從一般的非線性跟車模型可以看出,滯後時間T(h(t))實質上是由跟車車輛的車間距h(t)決定的,對於這種表現滯後時間和狀態有關的微分系統的特點之一就是有可能出現因果倒置關係的出現,即先輸入的信號後有輸出,而後輸入的信號先有輸出。
基本介紹
跟車模型,GHR模型建立,跟車理論的套用,非線性跟車模型及其跟車模型的一般形式,
跟車模型
跟車模型(Carfollowingmodels)是運用動力學方法研究在無法超車的腳踏車道上車輛列隊行駛時後車跟隨前車的行駛狀態,並用數學形式表達同時加以分析闡明的一種微觀模型。其主要目的是通過觀察各個車輛逐一跟駛的方式來了解腳踏車道交通流的特性。通過求解跟車方程,可以得到任意時刻車隊中各車輛的速度、加速度和位置,用於分析車隊的安全狀況,在此基礎上,提出改進車隊安全的措施,如給駕駛人提供較多的信息、設法減少駕駛人的反應時間等。
運用跟車模型可以分析交通流穩定性,包括局部穩定性和漸進穩定性。對於穩定性的研究具有特殊意義,它有助於解釋引起追尾事故和交通堵塞的原因,同時也可用於隧道等瓶頸路段車流特性的分析與改進。跟車模型在20世紀60年代就被用於評估駕駛人輔助系統、研究公共汽車車隊特性等方面。當前在智慧型交通系統,如自動巡航系統的開發中,相關學者也對車輛的跟車模型進行了大量細緻的研究,以保證自動控制下的車輛在跟隨過程中能安全而平穩地行駛。
跟車模型的另一重要套用是交通仿真,在20世紀80年代後期以來所進行的跟車模型研究,基本上都是基於開發交通流仿真模型或是模擬駕駛。根據不同的開發目的,跟車模型各有特點,如專門用於城市道路交通仿真的跟車模型注重對城市交通中車輛反覆停車一起步的模擬;基於自動巡航系統的仿真注重對,人機操作界面的模擬;對智慧型交通系統中的駕駛模擬則注重對駕駛人的信息接受與處理的模擬等。通過對各種交通流的仿真,可以進行交通改進措施、交通管制方案的評價以及道路通行能力研究和交通政策評價等方面的工作。
按照建模原理的不同,跟車模型可分為刺激—反應模型、安全距離模型、心理—生理模型和基於模糊邏輯的跟車模型四種主要模型。
GHR模型建立
刺激一反應模型的雛形最早由Reuschel和Pipes分別單獨提出,其早期形式為假設駕駛人試圖調節本車速度以與前車速度相一致。根據兩個公認的假設:(1)駕駛人將考慮本車與前車的速度差調節車速;(2)駕駛人存在反應延遲,建立如下車輛行駛動力學方程:
an+1(t+T)=cΔvn,n+1(t)
其中,an+1(t+T)表示t+T時刻第n+1輛車(後車)的加速度,Δvn,n+1表示t 時刻第n輛車(前車)與第n+1輛車之間的速度差(相對速度),T為駕駛人的反應時間,c為待定比例參數。
20世紀50年代由通用汽車研究實驗室的Chandler.Herman和Montroll對該模型進行了實驗分析,測試8輛車跟隨一輛“理想”速度變化(從15km/h~120km/h之間變化)的前導車的反應情況,車輛之間用金屬線連線以測量車間距和相對速度,試驗持續了30min。試驗數據表明,加速度與速度差具有明顯的相關性(r>0.8),但待定比例參數c和反應時間T的變化幅度較大,變化區間分別為0.17~0.74s和1.0~2.2s,不能認定為常數。
Gazis、Herman和Rothery引入了“反應=靈敏度x刺激”的心理學公式,並對靈敏度項進行改進,增加了車間距和本車速度兩個影響因素,構成如下非線性跟車模型(常被稱為CHR模型):
an+1(t+T)=cvn+1(t+T)Δvn,n+1(t)/cΔxn,n+1(t)
其中,vn+1(t+T)表示t+T時刻第n+1輛車的速度,Δxn,n+1(t)表示t時刻第n輛車與第n+1輛車之間的距離,m、l為待定的冪次參數。
這個模型由於增加了車間距和本車速度兩個因素,以及m、l兩個待定的冪次參數,使得該模型更具有通用性,不僅能針對不同地區和駕駛環境下的駕駛行為進行建模,還可以通過選擇m、l的不同組合區分加速、減速、剎車或者平穩駕駛等不同狀態分別建模。隨後有大量學者對該模型進行了研究,嘗試標定m、I之間的最佳組合。
此外,一些學者也提出了其他形式的刺激一反應模型。一類是建模集中在模型右側項的形式,如考慮速度差與車間距的線性加權組合形式、增加前後車當前時刻加速度的線性組合等。另一類是受Herman、Montroll和Potts提出的多輛前車思路的啟發,即駕駛人不僅考慮正在跟隨的那輛前車,而且通常同時考慮兩輛以上的前車,從而建立各種形式的雙前車跟車模型。
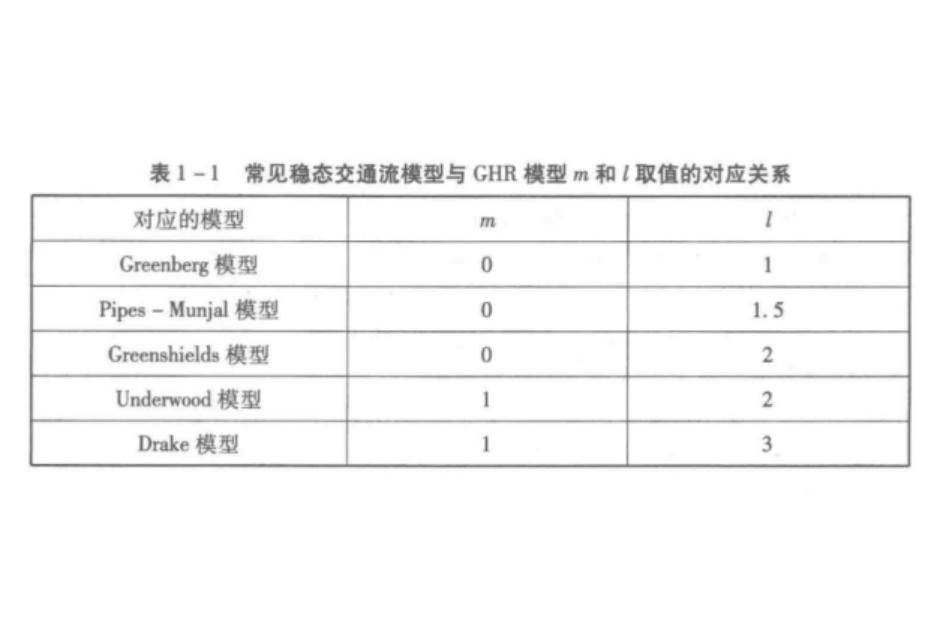
刺激一反應模型的一個重要特性是可以通過積分導出穩態交通流模型,在動態微觀交通流模型和穩態巨觀交通流模型之間建立了橋樑,從而在某種程度上印證了這些不同來源的理論的合理性。常見的穩態交通流模型和CHR模型中m、l取值的對應關係參見下表。
刺激一反應模型由於是最早的跟車模型而具有開創意義,之後提出的許多跟車模型都源於它所建立的刺激一反應基本關係。同時它形式簡單、物理意義明確。但是隨著對這一領域的深人研究,其模型對於複雜交通現象的描述還不能令人滿意,因此還需進一步研究和改進。在交通仿真軟體TransMod-eler及其前身MITSIM中跟隨駕駛狀態採用了改進的CHR模型。
跟車理論的套用
2)依據跟車理論可尋求車輛跟車運動的規律,估計車流中前、後車之間的相互影響。為了維持與行車速度相適應的車頭間距,而不致過小,交通管理中可根據道路交通環境和氣候條件,控制車流量不超過規定的交通量,避免因流量過大,後車緊迫前車,形成追隨間隔縮小,造成一連串的尾撞事故的發生。在交通規劃與交通管理中,可以此作為依據進行流量分配,使路網交通量的分布,不超過規定的交通量數值。
3)依據跟車理論,在道路交通管理中設法使前車給後車駕駛員提供較多的信息,如提供車頭間距、相對速度等信息,以減少反應時間,幫助駕駛員跟隨車輛安全行駛,防止尾撞事故的發生。
4)通過計算機模擬車隊的跟車狀態,研究車輛跟車運行中的安全性。若能將道路交通系統中的駕駛員反應時間、車頭間距和相對速度的臨界值三個參數減至最少,便可增強駕駛員的感覺,縮短駕駛員反應的延滯時間,以減少交通事故。
5)通過跟車理論可分析公共汽車的腳踏車道流量。跟車試驗的穩定性分析表明:所有的數據點都在漸近穩定區內,且驗證了公共汽車跟車模型的預測;平均速度為53km/h,測出的公共汽車最大流量為1450veh/h。
通過跟車模型試驗可預測小型汽車,駛入市區環路、幹路的車流對市內交通的影響。
6)由跟車模型的一般形式,當參數m和l取各種不同的組合時,經積分確定邊界條件,推導出各種不同的交通流模型。
非線性跟車模型及其跟車模型的一般形式
線性跟車模型的特點是簡便和對穩定分析的敏感性,但它的明顯缺點是跟隨車的反應(加速度)僅為兩車相對速度的函式,而與車輛的間距無關。
1959年,伽賽斯(Gazis)等人採用靈敏度係數與車頭間距成反比的關係,得到了非線性跟車模型:
xˊˊn+1(t+T)=[a/[xn(t)-xn+1(t)]]·[xˊn(t)-xˊn+1(t)]
式中 a——比例常數,單位是距離/時間;
xi(t)——第i輛車在時刻t的位置。
根據伽賽斯的推導出——a=Vm=1/2Vf
由非線性跟車模型可以看出,靈敏度與交通流的臨界車速成正比,與‘時刻兩車間的距離成反比。這是符合實際情況的,因為車隊的速度愈快,跟隨車輛駕駛員的靈敏度也應愈高,否則車速高,制動距離長,易發生尾撞事故;而兩車間的距離愈大,留給跟車駕駛反應、採取行動的時間愈長,即使駕駛員的靈敏率低些、反應時間長一點,也不會發生尾撞事故。
在1961年,伽賽斯又提出了跟車理論的一般形式
xˊˊn+1(t+T)=[axˊn+1(t+T)/[xn(t)-xn+1(t)]]·[xˊn(t)-xˊn+1(t)]
式中axˊn+1(t+T)/[xn(t)-xn+1(t)]為靈敏度;m,l為常數。
當m=0和l=0時,上述通式就成為線性模型公式;當m=0,l=1時,成為非線性模型公式。
跟車模型的一般形式還表明,靈敏度除了與交通流臨界車速成正比,與兩車間距離成反比之外,還與(t+T)時刻後車的速度成正比。因為後車的車速愈高,要求駕駛員的反應、敏捷水平也應愈高,否則會發生尾撞事故。