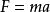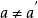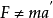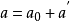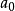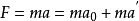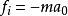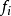基本介紹
慣性參考系,非慣性參考系,平移慣性力,離心慣性力,科里奧利力,慣性力是真是假,
慣性參考系
對一切運動的描述，都是相對於某個參考系的。參考系選取的不同，對運動的描述，或者說運動方程的形式，也隨之不同。人類從經驗中發現，總可以找到這樣的參考系：其時間是均勻流逝的，空間是均勻和各向同性的；在這樣的參考系內，描述運動的方程有著最簡單的形式。這樣的參考系就是慣性參照系，也稱為慣性參考系或慣性系。
非慣性參考系
平移慣性力
參考系相對於慣性系運動，固定於該參考繫上直角坐標系的原點作變速直線運動，且各坐標軸的方向始終保持不變。
例如：向右加速運動的小車是一非慣性系，是一直線加速參考系。 討論：小球的運動狀態：（桌面光滑）
（1）以地面為參考系：小球水平方向不受力，靜止。
（2）以小車為參考系：小球相對於車向左以加速度
運動，由於水平方向不受力，不符合牛頓第二定律。
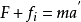
通過引入虛擬力（這裡稱“平移慣性力”）可將牛頓第二定律推廣到了非慣性參考系。
引入“慣性力”，對於小車非慣性系，仍可用牛頓第二定律的形式。小球相對於車身的加速度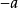
是慣性力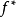
作用的結果。總之：在直線加速運動的非慣性系中，質點所受慣性力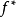與非慣性系的加速度a方向相反，且等於質點的質量m與非慣性系的加速度a的乘積。
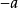
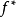
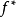
直線加速參考系中的動力學方程
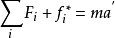
其中
是真實力，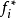
是平移慣性力，此式即為質點在直線加速參考系中的動力學方程。
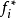
“虛擬力”與“真實力”的區別
（1）不能指出是哪個物體作用 ；
（2）沒有反作用力；
（3）所有質點都受力；
（4）虛擬力可以消除。
離心慣性力
如圖所示：圓盤以勻角速率繞鉛直軸轉動，圓盤上用長為r的線將質量為m的小球繫於盤心且相對於圓盤靜止。
對於觀察者1：從慣性系看：小球受線拉力的作用下做勻速圓周運動，符合牛頓第二定律，有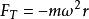
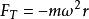
對於觀察者2：從圓盤非慣性系看：小球受到拉力的作用，卻保持靜止，不符合牛頓第二定律。
故有：相對於慣性系做勻速轉動的參考系也是非慣性系。
引入慣性力：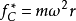
——離心慣性力
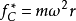
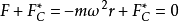
上式的力稱為離心慣性力, 是自轉軸向質點所引的矢量，與垂直。即：若質點靜止於勻速轉動的非慣性系中，則作用於此物體所有相互作用力與離心慣性力的合力等於零。
科里奧利力
若質點相對於轉動的參考系運動，則質點還可能受到科里奧利力。
定性說明：
效應一：
圖一，物體相對地面沿直線OABC運動圖二，物體相對轉盤沿曲線OA´ B´C3´ 運動
效應二：
圖三，物體相對轉盤沿直線OA’B’C’運動圖四，物體相對地面沿曲線OABC 運動
物體相對慣性系作曲線運動，表明物體必受真實力作用. 物體所受真實力與物體所受慣性力大小相等、方向相反。
定量表述：
如圖示：一圓盤繞鉛直軸以勻角速率ω 轉動，盤心有一光滑小孔，沿半徑方向有一光滑槽，其中質一小球m，可視作質點，以細線連之，線另一端穿過小孔，可控制小球在槽中作勻速運動，速度為v（相對）沿槽向外運動，經時間△t，圓盤轉過ω△t 角，而小球自A運動至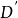
。
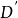
從地球慣性參考繫上研究：
A點，小球的速度：v（相對）和切向速度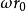
，
為A點處的半徑，二者合成應使小球達到D點，實際上小球到達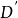點，這表明槽對小球的作用有沿切線或圓弧方向的力，使小球獲得切向加速度，使小球多走出弧長
。
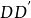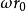
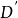
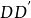
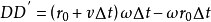
由於△t 很短，可設小球以恆定加速度
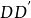走出，於是有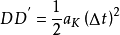
，
是槽壁作用於小球的推力產生的。
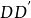
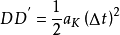
考慮物體相對地面走的是曲線，則相對轉盤走的是直線，設物體相對轉盤速度為
，則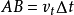
，
，
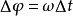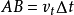
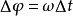
設物體向右方的加速度為，有
則有
——科里奧利加速度
質點相對轉盤走的是直線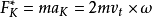
——科里奧利力
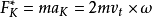
從非慣性繫上研究：
小球的受力：線的拉力T，離心慣性力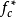
，二者平衡，槽對球的推力；但並沒發生與槽垂直的運動，故還受一慣性力：
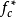
註：若質點相對於勻速轉動的圓盤作變速轉動，則慣性力為：離心慣性力和科里奧利力。
科里奧利力特徵
（1）與相對速度成正比，故只有當物體相對轉動參考系運動時才能出現；
（2）與轉動角速度的一次方成正比；
（3）力的方向總是與相對速度垂直，不會改變相對速度的大小。
地球上的表現
（1）地面上北半球河流沖刷右岸，火車對右軌的偏壓較大， 南半球則相反；
（2）地球上自由落體偏東；
（3）傅科（J.L.Foucalt）擺直接證明地球自轉；
（4）天氣圖上，高、低氣壓環流能長期存在。
慣性力是真是假
在導出非慣性系中運動定律的形式表示的過程中，不時冠以虛擬力或假想力之定語於慣性力，以與真實作用力相區別，那是為了免除初學時概念上的混淆。其實，慣性力所產生的物理後果是真實的，慣性力也可以由測力器測出。過分強調慣性力的假想性，這在物理思想上是要被質疑的。
愛因斯坦於1915年創立了廣義相對論的理論基礎，其基本原理之一—— 等效原理，最初表述是，引力與慣性力實際上是等效的，即慣性力與引力對一切物理現象的影響都應該是不可區分的。
