霍爾斯特德複雜度量測（Halstead complexity measures）是由霍爾斯特德在1977年提出的一種軟體度量方法。是有關軟體開發經驗科學的論文中的一部分。
基本介紹
- 中文名：霍爾斯特德複雜度量測
- 外文名：Halstead complexity measures
- 性質：軟體度量方法
- 領域：計算機
簡介,計算,循環複雜度,
簡介
霍爾斯特德的目標是識別軟體中可量測的性質，以及各性質之間的關係。有點類似識別物體中可量測的性質（如氣體的體積、質量及壓強），以及各性質之間的關係（如理想氣體方程式的體積、質量及壓強），因此霍爾斯特德複雜度量測不單單只是一種程式複雜度的度量。
計算
針對特定的算法，首先需計算以下的數值：
1.
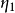為不同運運算元的個數。
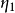
2.
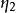為不同運算元的個數。
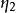
3.
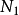為所有運運算元合計出現的次數。
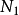
4.
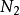為所有運算元合計出現的次數。
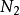
上述的運運算元包括傳統的運運算元及保留字，運算元包括變數及常數。
依上述數值，可以計算以下的量測量：
1.程式辭彙數（Program vocabulary）：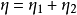
。
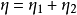
2.程式長度（Program length）：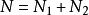
。
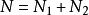
3.計算程式長度（Calculated program length）：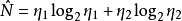
。
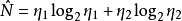
4.容量（Volume）：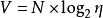
。
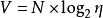
5.難度（Difficulty）：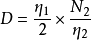
。
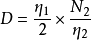
6.精力（Effort）：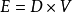
。
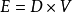
難度量測和撰寫程式或是了解程式（例如代碼審查時）的困難度有關。 精力可以用以下的關係式轉換為實際的程式撰寫時間。
程式撰寫時間：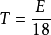
秒。
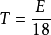
霍爾斯特德交付錯誤（Halstead's delivered bugs）是估計在實現過程中會產生的錯誤。
交付錯誤數量（Number of delivered bugs）：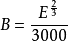
，或者是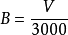
。
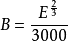
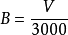
循環複雜度
循環複雜度（Cyclomatic complexity）也稱為條件複雜度或圈複雜度，也是一種軟體度量，是由老托馬斯·J·麥凱布在1976年提出，用來表示程式的複雜度，其符號為VG或是M。循環複雜度由程式的原始碼中量測線性獨立路徑的個數。此概念有些類似的量測文字複雜度的Flesch-Kincaid可讀性測試，不過方法不完全相同。
“循環複雜度”的名稱有時會讓人誤解，因為此複雜度不只計算程式中的循環（循環）個數。循環複雜度是指程式的控制流圖中，若將結束點到啟始點再增加一個邊時，控制流圖中的圈（幾個邊形成封閉路徑）的個數。
