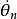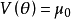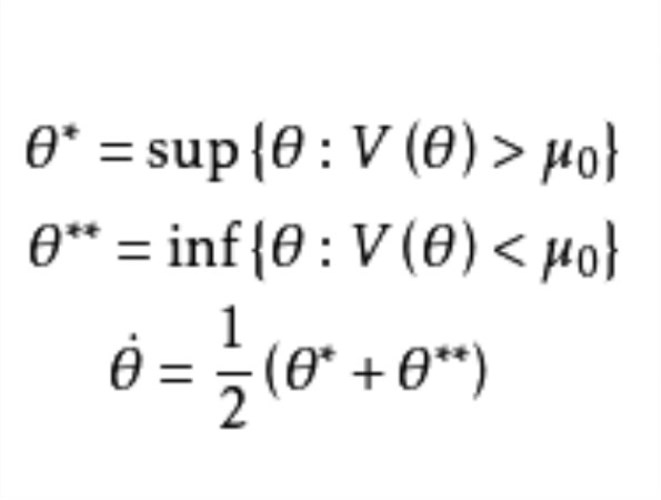基本介紹
- 中文名:霍奇斯-萊曼估計
- 外文名:Hodges-Lehmann Estimation
- 所屬學科:數學(統計學)
- 適用條件:觀測值有可加性誤差時
- 提出者:Hodges-Lehmann
基本介紹,相關分析,基於符號檢驗的估計,Hodges-Lehmann估計,
基本介紹
霍奇斯-萊曼估計(Hodges-Lehmann估計)是指兩個沒有刪失的數據樣本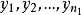 和
和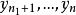 之間位置差的估計量,其中
之間位置差的估計量,其中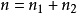 ,定義霍奇斯-萊曼估計量為:
,定義霍奇斯-萊曼估計量為:
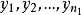
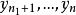
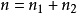
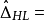
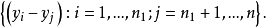
相關分析
基於符號檢驗的估計
設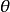 是總體分位數,考慮假設
是總體分位數,考慮假設
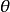
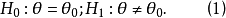
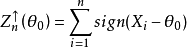
對取定的顯著水平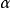 ,有k滿足,
,有k滿足,
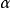
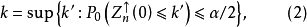
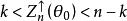
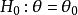
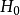
由利用檢驗函式構造置信區間的方法,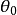 的置信度為
的置信度為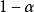 的置信集為:
的置信集為:
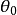
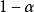
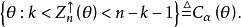
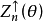
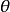
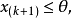
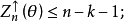
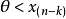
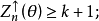
於是 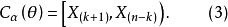
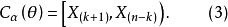
由(2)
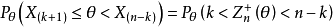
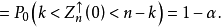
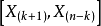
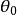
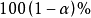
由(3)確定的區間長生,隨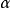 的增加而減小,當
的增加而減小,當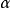 =1—0時,區間長度達到最短。它的中點
=1—0時,區間長度達到最短。它的中點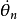 可做為
可做為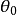 的點估計。易見,這最短區間為
的點估計。易見,這最短區間為
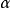
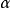
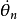
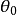
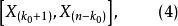
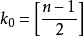
即
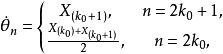
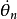
不難驗證,區間(4)的端點滿足,
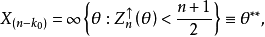
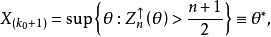
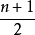
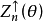
Hodges-Lehmann估計
將上述確定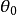 的估計方法推廣到一般情形,就得到所謂Hodges-Lehmann估。給定定義如下:
的估計方法推廣到一般情形,就得到所謂Hodges-Lehmann估。給定定義如下:
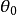
設X1,X2,…,Xn是抽自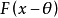 的簡單樣本。F(x)連續,在原點鄰域內嚴格增,且
的簡單樣本。F(x)連續,在原點鄰域內嚴格增,且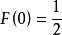 。
。
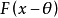
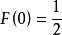
設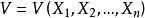 是檢驗假設
是檢驗假設
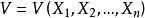
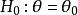
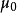
令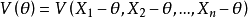
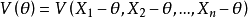
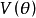
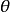
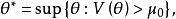
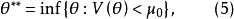
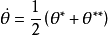
進而,令
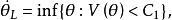
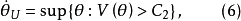
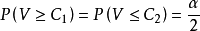
則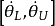 是
是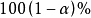 的基於V的置信區間。
的基於V的置信區間。
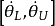
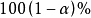
直觀地講Hodges-Lehmann估計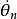 可視為方程
可視為方程