電路拓撲又稱電路的圖，即電路結構，是對電路圖進行再次抽象、僅由支路和結點構成的一個集合，它討論的是電路的連線關係及其性質，即支路與結點的連線關係。
基本介紹
- 中文名：電路拓撲
- 外文名：circuit topology
- 定義：電路結構
- 討論點：支路與結點的連線關係
- 又稱：電路的圖
- 套用學科：網際網路
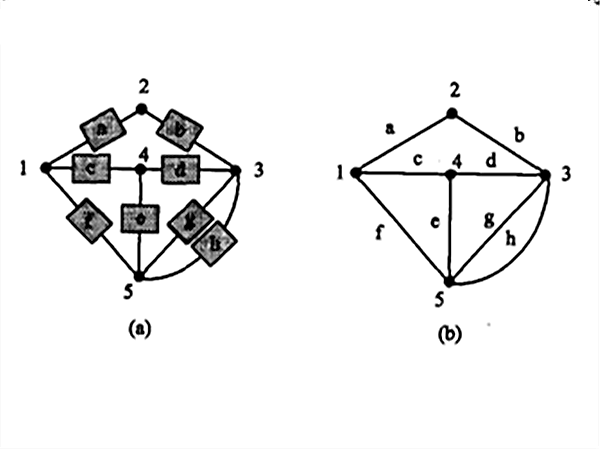
定義,電路拓撲約束,基爾霍夫電流定律,基爾霍夫電壓定律,相關名詞,
定義
由於拓撲約束與元件的特性無關，在研究拓撲約束時，我們可以將電路中的元件用線段代替，畫成一些由線段組成的圖，如將右圖中的（a）電路圖畫成（b）拓撲圖。
我們稱右圖（b）為（a）所示電路的“圖”，圖中的各線段稱為支路，線段的連線點稱為節點。因此，圖的確切定義是：一組節點與支路的集合，其中每一支路的兩端都終止在節點上。在上圖中，a，b，c，d，e，f，g，h為支路，1，2，3，4，5為節點。
在圖中構成一個閉合路徑所需的數量最少的支路集合稱為迴路，在迴路中去掉一個支路則不能構成閉合路徑。在一個圖中可以有許多迴路。如果迴路中不包圍其他支路，則稱這樣的迴路為網孔。如果在圖上標明各支路電流(或電壓)的參考方向(通常採用電壓和電流的一致參考方向來同時表示電壓和電流），這樣的圖則稱為有向圖。
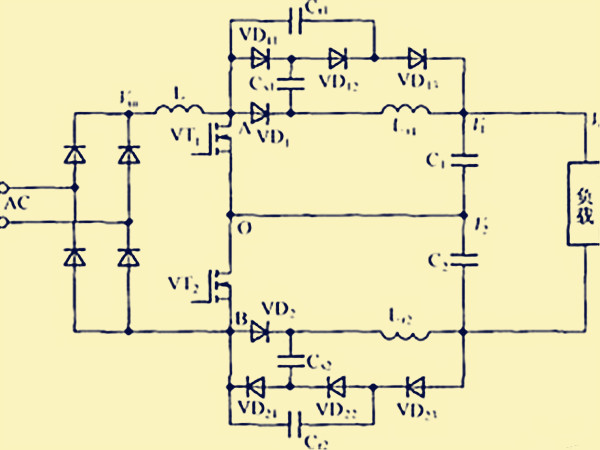
電路拓撲又稱電路的圖，即電路結構，是對電路圖進行再次抽象、僅由支路和結點構成的一個集合，它討論的是電路的連線關係及其性質，即支路與結點的連線關係。
電路拓撲約束
基爾霍夫電流定律
基爾霍夫電流定律(Kirchhoff's Current Law，KCL)描述電路中流入(流出)同一個結點的電流之間的關係，其內容為：任一時刻，流出集總參數電路中任一結點的電流代數和為零，KCL表達式為
。
規定流出結點的電流取正號，流入結點的電流取負號。
KCL定律內容的另外兩種闡述方式為：
任一時刻，流入集總參數電路中任一結點的電流代數和恆為零。
規定流入結點的電流取正號，流出結點的電流取負號。
任一時刻，流人集總參數電路中任一結點的電流之和等於流出該結點的電流之和。
規定流入節點的電流
取正號相加等於流出結點的電流
取正號相加。
KCL的實質是電荷在結點處，既不能積累，也不能減少。同時，可以把KCI推廣到包含幾個結點的封閉面，稱其為超結點(Supernode)。
基爾霍夫電壓定律
基爾霍夫電壓定律(Kirchhoff’s Voltage Law，KVI)描述電路中繞行同一個迴路一周的電壓之間的關係，其內容為： 任一時刻，沿集中參數電路的任一迴路繞行一周。各電壓降的代數和恆為零。KVI的表達式為
。
例如電路右圖所示，首先指定迴路繞行方向為順時針。然後查看各電壓的參考方向與迴路繞行方向是否一致，若電壓參考方向與迴路繞行方向一致，為電壓降。前面取正號；否則取負號。得到
。
KVI的實質是電位單值性，即繞行迴路一周必然進入與離開組成該迴路的每個結點各一次。而電壓是兩個終點電位之差。因此，繞行迴路一周，電壓降的代數和必為零。
相關名詞
如果電路中兩個結點(稱為始端結點和終端結點)間存在由不同支路和不同結點依次連線而成的一條通路，則稱為這條通路為連線該兩點的路徑(path)。路徑可以用支路集合或結點集合來表示。例如右圖中，支路集合{2，4)或結點集合{①，②，③)都表示始端結點①和終端結點③之間的路徑。兩個結點之間可以存在多條路徑，顯然支路集合{1，3，4)或結點集合{①，④，②，③}也表示始端結點①和終端結點③之間的路徑。電路中任一閉合的路徑稱為迴路(100p)。如右圖所示中支路集合{1，2，3)、{3，4，5，6}、{1，2，4，5，6)都是迴路。可以為迴路規定方向(順時針或逆時針)，一般用箭頭或集合中元素的順序表示迴路的方向。
如果將電路畫在平面上，可以做到任意兩條支路都不相交的情況，那么稱電路為平面電路(planar circuit)。平面電路中的單孔迴路(即在迴路內部或外部不另含支路)稱為網孔(mesh)。內部不含任何支路的網孔稱為區域網路孔；外部不含任何支路的網孔稱為外網孔。在圖1．7中，支路集合{1，2，3}、{3，4，5，6)表示兩個區域網路孔，而支路集合{1，2，4，5，6)表示外網孔。如無特別講明，網孔均指區域網路孔。
