電矩

電矩（electric moment），電偶極矩的簡稱。在物理學里，電偶極矩衡量正電荷分布與負電荷負電荷分布的分離狀況，即電荷系統的整體極性。

基本介紹

• 中文名：電矩
• 外文名：electric moment
• 全稱：電偶極矩
• 定義：從-q指向+q的矢徑r和電量q的乘積
• 數學表達式：p=qr
• 物理意義：電荷系統的極性的一種衡量

概況

連線+q和-q兩個點電荷的直線稱為電偶極子的軸線，從-q指向+q的矢徑r和電量q的乘積定義為電偶極子的電矩，也稱電偶極矩，通常用矢量p表示。電偶極矩的物理意義是對電荷系統的極性的一種衡量。在兩個點電荷的簡單情形中，一個帶有電荷 + q，另一個帶有電荷 -q，則電偶極矩為：p=qr。

其中r是從負電荷指向正電荷的位移矢量。這意味著電矩的矢量從負電荷指向正電荷。注意到電場線的方向是相反的，也就是說，從正電荷開始，在負電荷結束。這裡並沒有矛盾，因為電偶極矩與電荷的位置有關，與電場線無關。

特徵

更一般地，對於任意數目的點電荷的系統，電矩為：

其中每一個r_i是一個矢量，從某一個參考點指向電荷q_i的值與參考點的選擇無關，只要整個系統的總電荷為零。這個公式在n = 2時，與前一個公式是等價的。電矩矢量從負電荷指向正電荷的事實，與一個點的位置矢量是從原點指向該點的事實有關。

對於電中性系統

當整個系統是電中性時，電偶極矩最容易明白，例如一對相反的電荷，或位於均勻電場內的導體。對於這類系統，電偶極矩的值與參考點的選擇無關。

對於非電中性系統

在討論非電中性的系統，例如質子的電偶極矩時，則與參考點的選擇有關。在這種情況下，通常把參考點規定為系統的質心，而不是任意一個點。這個規定保證了電偶極矩是系統的一個固有的性質。

分子電偶極矩測定

電矩與極化度

分子呈電中性，但因空間構型的不同，正負電荷中心可能重合，也可能不重合。前者稱為非極性分子，後者稱為極性分子，分子極性大小用偶極矩μ來度量，電矩定義為：

式中，q為正、負電荷中心所帶的電荷量；d是正、負電荷中心間的距離。偶極矩的SI單位是庫侖·米（C·m）。

若將極性分子置於均勻的外電場中，分子將沿電場方向轉動，同時還會發生電子云對分子骨架的相對移動和分子骨架的變形，稱為極化。極化的程度用摩爾極化度P來度量。P是轉向極化度P_轉向、電子極化度P_電子與原子極化度P_原子之和：P=P_轉向+P_電子+P_原子……

由於P_原子在P中所占的比例很小，所以在不很精確的測量中可以忽略P_原子，則上式可寫成：P=P_轉向+P_電子。只要在低頻電場V或靜電場中測得P；在V的高頻電場（紫外可見光）中，由於極性分子的轉向和分子骨架變形跟不上電場的變化，故P_轉向=0。

P_原子=0，所以測得的是P_電子。這樣可求得P_轉向，再計算μ。

通過測定分子電矩，可以了解分子中電子云的分布和分子對稱性，判斷幾何異構體和分子的立體結構。

溶液法測定電矩

所謂溶液法就是將極性待測物溶於非極性溶劑中進行測定，然後外推到無限稀釋。

本實驗是將正丁醇溶於非極性的環己烷中形成稀溶液，然後在低頻電場中測量溶液的介電常數和溶液的密度求得摩爾極化度；在可見光下測定溶液的摩爾折射度，然後計算正丁醇的偶極矩。

實驗裝置如下圖：左邊是精密電容測量儀，中間是電容池，右邊是阿貝折射儀。

電矩的計算

鏡像法

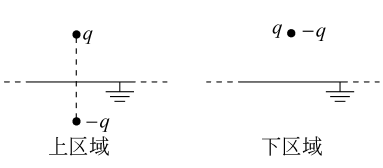
首先求解金屬板上、下方的電場，這一問題可利用鏡像法來求解。如圖所示，板上方的電場是點電荷q與位於金屬板下方且位置與q相對於金屬板對稱的點電荷- q(鏡像電荷)產生的電場的疊加；板下方的電場是點電荷q與位於金屬板上方且位置與q重疊的點電荷- q(鏡像電荷)產生的電場的疊加，即為零。由高斯定理(高斯面為上表面是金屬板上表面、下表面位於金屬板內部或下方的無限大柱形面)可知，金屬板上的感應電荷即等於通過金屬板的上表面的電位移矢量通量(法線方向向上)。這一通量可採用微積分的方法來計算，但計算比較麻煩，現介紹一種簡便方法。過點電荷q作一個與金屬板平行的平面，則從這一點電荷發出的位於這一平面下方的電場線均要射向金屬板，而從這一點電荷發出的位於這一平面上方的電場線則不會。所以，點電荷q產生的電場通過金屬板上表面的電位移矢量通量等於-12q(金屬板上表面的法線向上)；同理，點電荷- q產生的電場通過金屬板上表面的電位移矢量通量也等於-12q，因此，金屬板上區域的電場通過金屬板上表面的通量等於- q，這也就是金屬板上的感應電荷。

首先求導體球以外區域的電場，如下圖所示，用鏡像法求解可知，導體球以外區域的電場是點電荷Q和位於導體球內與球心O的連線上距球心O為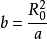 的點電荷 (鏡像電荷)產生的電場的疊加。那么，由於點電荷Q所產生的電場通過導體球的通量為零，故球外電場通過導體球的通量即為點電荷Q′所產生的電場通過導體球的通量，根據高斯定理(高斯面為導體球表面)可知，導體球上的感應電荷即為Q′。導體球以外區域的電場,仍用鏡像法求解。

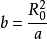
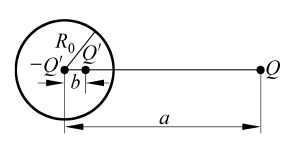
這裡，導體球是一電勢不等於零的等勢體，所帶電荷為零。由球外區域電場的答案可知，只要在球心O處放一點電荷- Q′，則這樣分布的3個點電荷Q、Q′、- Q′在球外區域所產生的電場即符合所求場的邊界條件，由惟一性定理可知，3個這樣分布的點電荷Q、Q′、- Q′在球外區域所產生的電場即是所求場的解，如圖所示，根據高斯定理(高斯面為導體球表面)可知，導體球上總的感應電荷為零，但是，導體球上的左面分布了- Q′的感應電荷，右面分布了Q′的感應電荷，它們所產生的電偶極矩為：

分離變數法

如圖所示，接地導體球與導體球殼之間的電場和導體球殼以外區域的電場，電勢滿足拉普拉斯方程，可用分離變數法求解，電勢的解為

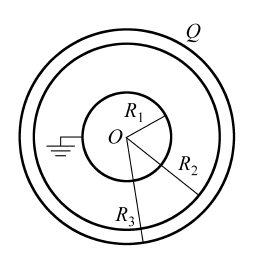
其中：

根據高斯定理(高斯面為導體球表面)可知，導體球上的感應電荷為

導體球殼上的電荷分布將是內球殼上帶- Q₁的電荷，外球殼上帶Q+ Q₁的電荷。

綜上所述，本類問題求解的一般方法就是先求出靜電場的解，再由高斯定理求出導體上的感應電荷或電偶極矩。