雷射與生物組織相互作用

雷射與生物組織相互作用，分為可逆的作用和不可逆的作用兩種情況。

雷射作用於生物組織發生可逆反應的情況下，包含了多種相互作用，包括散射、吸收、反射等。不同的生物組織由於其光學特性的不同，對雷射作用的應答性反應也會不同。在組織的光學特性中，最重要的是反射、吸收及散射係數，它們共同決定了某一波長的光在組織中的傳輸情況，而“組織光學”（Tissue Optics）正是基於此研究領域發展起來的，是研究光輻射能量在生物組織體內的規律以及有關組織光學特性的測量方法的一門新興交叉學科。

不可逆的作用則主要分為5種類型：光化作用（photochemical interaction），熱相互作用（thermal interaction），光蝕除（photoablation），電漿誘導蝕除（plasma-induced ablation）和光致破裂（photodisruption）。基於此方面的研究則主要用於疾病的治療。

1.雷射與生物組織發生可逆相互作用

1.1光學特性的基本原理

光在傳播過程中碰到物質會發生的現象包括反射、折射、散射和吸收。圖1為光束入射薄片物質上的一些典型情況。

圖1 反射、折射、吸收和散射現象

1.2 組織中光傳輸

目前研究光在生物組織中的傳輸主要有兩種理論：電磁理論和輻射傳輸理論。電磁理論以麥克斯韋方程為基礎，考慮介質的統計特性及光的波動性，從原理上講它是最基本的方法，包含所有的衍射效應；其不足之處在於數學上過於複雜，使其在實際套用中受到限制，唯有在微米尺度上研究組織散射特性時有所套用。輻射傳輸理論不直接從麥克斯韋方程出發，它忽略了光的波動性和生物組織的內在結構，直接處理了光能量在生物組織內的統計傳輸過程，雖然其缺乏電磁理論的嚴格性，但它有著良好的實驗基礎，適合絕大多數的光傳輸問題，因而在組織光學內得到了廣泛的套用。

在輻射傳輸理論中，生物組織被抽象成是一個由大量吸收和散射元的集合。這些吸收和散射元服從統計均勻分布，同時還忽略了光的波動性，僅考慮光能量在組織內的傳輸過程。此時，利用輻射傳輸理論得到的方程可以較好的描述光子及其攜帶的能量在生物組織內的統計平均傳輸過程。

一般情況下，輻射傳輸方程無法得到解析解，因此該理論也發展了多種近似理論和數值算法，分為級數展開，離散求解，隨機模型三類，分別以漫射近似理論、Kubelka-Munk理論和Beer-Lambert定律、蒙特卡羅方法和隨機遊走理論為代表。上述方法都是在給定初始值和特定邊界條件基礎上建立起來得，因此都有特定的適用條件。這裡，我們簡單介紹其中兩種方法，蒙特卡羅模擬（Monte Carlo simulation）和Kubelka-Munk理論。

1.2.1 蒙特卡羅模擬

蒙特卡羅方法以光子的隨機行走模型來模擬光在生物組織中的傳輸，理論上可以處理任何條件下的光傳輸問題，被認為是最接近實際的方法。早在1978年，Meier就提出了蒙特卡羅模型，並將蒙特卡羅方法引入了組織光學進行生物組織光傳輸問題的研究，在其後數十年，基於蒙特卡羅方法的研究已取得了巨大的成果。

蒙特卡羅模擬的基本思想是：套用吸收和散射現象來跟蹤光子通過混濁介質的光程。將光子兩次碰撞之間的距離設定為對數分布，用計算機產生的隨機數表示，通過對每個光子確定一個權值，並且在傳播過程中持續的減小權值來表示吸收現象。如果發生散射，則由給定的相函式和一個隨機數來確定一個新的傳播方向。當光子逃逸出組織模型或其權值低於某一確定閾值時，定義光子消亡，模擬過程結束。根據Meier的觀點，蒙特卡羅模擬主要由五個步驟組成：源光子的產生（source photon generation），軌跡的產生（pathway generation），吸收（absorption），消亡（elimination）和檢測（detection）。

為了克服蒙特卡羅模型計算量大的難題，1993年，R.Graaff和M.H.Koelink等提出了精簡的蒙特卡羅模型，即用一組光學參數(散射係數、吸收係數、各向異性因子)的模擬，推知其他參數條件下的光傳輸規律，這樣可節省了重複計算所需的大量時間。

1.2.2 Kubelka-Munk理論

Kubelka-Munk理論是由Kubelka和Munk提出的，局限於線性幾何的一種模型，它的參數通常用於醫學物理領域。Kubelka-Munk理論僅能處理漫射輻射，並且局限於散射遠遠超過吸收的情況。

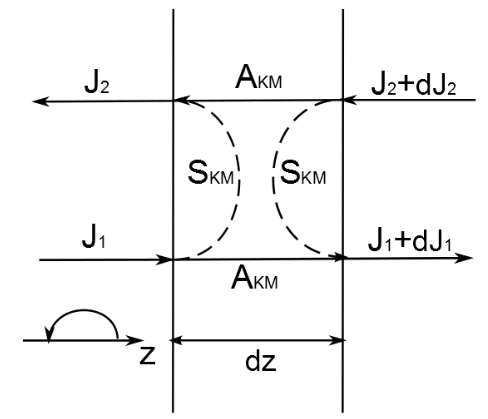
理論的假設前提是，輻射度完全是由漫射得到的，即J_c=0。圖2描述了在生物組織內可被區別的兩個漫射光通量的幾何圖形。在輻射光入射方向上的光通量為J₁，在相反方向上後向散射的光通量為J₂。

圖2 Kubelka-Munk理論兩個通量的幾何圖

有兩個Kubelka-Munk理論係數，A_KM和S_KM，它們分別被定義為吸收和散射漫射輻射。套用這些參數，可得到兩個微分方程：

式中，z代表的是入射輻射的平均方向。方程（1）和（2）通解可表示為：

其中，，Kubelka-Munk理論中最重要的問題是怎樣用來表示和。

Kubelka-Munk理論是一種被稱為多通量理論的特殊形式。在這個理論中，當考慮到在許多離散角上的輻射度時，傳輸方程就變成一個矩陣微分方程。除了Kubelka和Munk提到的兩個方向上的通量外，在其他理論中還涉及到更多的光通量，但所有這些多通量理論，都局限於一維幾何結構，並且假設入射光已被漫射，同時它的計算量也非常大。

2. 雷射與生物組織發生不可逆相互作用

雷射與組織不可逆的相互作用主要被分為5種類型：光化作用（photochemical interaction），熱相互作用（thermal interaction），光蝕除（photoablation），電漿誘導蝕除（plasma-induced ablation），光致破裂（photodisruption）。

2.1光化作用

光化作用，即大分子或是生物組織內，光可以引起化學作用和化學反應，比如光合作用引起的能量的釋放。在雷射醫學物理領域的光動力學療法（photodynamic therapy）中，光學作用機理起著很重要的作用。

在低功率密度（典型功率為0.01~50W/cm）和長時間曝光下（秒以上或者連續照射），光化作用就會發生。在多數實例中，普遍選擇波長在可見光範圍內的雷射器，因為其具有較高的發光效率和高的光穿透深度。

2.2熱相互作用

光熱作用主要是組織吸收雷射能量後轉為為熱能，導致組織溫度升高，根據組織的不同反應，可以分為凝結、汽化、碳化和熔融，主要套用於治療視網膜脫落 ，雷射誘導間質熱療法等。

熱產生是由雷射參數和生物組織的光學性質決定的。這些性質主要是指輻照度、曝光時間及吸收係數。這裡採用的典型脈衝持續時間為1微秒至1分鐘，典型功率密度為10~10W/cm。熱傳輸完全由熱導率和熱容量等生物組織熱血特性表征。熱效應最終依賴於生物組織的類型和生物組織內所達到的溫度。

2.3 光蝕除作用

光蝕除是當某種材料在高強度雷射的照射下，產生分離的現象。光蝕除作用的物理原理是組織吸收高能量的紫外的光子，然後被提高到互相排斥的激發態，這時共價鍵離解，而組織不壞死，這樣就達到了蝕除的目的。它的優點是切割的精準性、極好的可預測性和對鄰近組織的無熱損傷性。它的脈衝持續時間是10~100ns，典型的功率密度是10至10W/cm。

2.4 電漿誘導蝕除

當固體和流體得到超過10W/cm功率密度，或氣體得到10W/cm的功率密度時，就會發生光擊穿現象。當雷射參數選取合適時，用電漿誘導蝕除法，就可以得到光滑的、輪廓清晰的組織分離，而不會產生任何熱損傷或機械損傷。電漿誘導蝕除也被稱為電漿傳遞分離。典型脈衝持續時間為100fs~500ps，而功率密度範圍為10—10W/cm。電漿誘導蝕除主要套用於角膜屈光手術。

2.5光致破裂

當脈衝能量很高時，衝擊波和其他機械方面的影響就變得很重要，這就導致了一種新的作用—光致破裂。與光致破裂作用有關的物理效應是電漿的形成和衝擊波的產生。它將雷射能量轉換成機械能而產生高衝擊力的衝擊波，這種衝擊波靠其強有力的衝擊力來粉碎組織。

光致破裂的主要決定因素是雷射峰值功率、脈衝寬度、脈衝強度以及雷射光束的聚焦程度，可通過調節這些參數來獲得預期結果。一般情況下，脈衝持續時間為100fs~100ns，典型功率密度為10—10W/cm。光致破裂最主要的套用是晶狀體切開術，同時還可以用於泌尿系統結石的雷射誘導碎石術中。

擴展閱讀

[1] 謝樹森，雷仕湛.2004.光子技術.北京：科學出版社

[2] 姚翠萍，張鎮西.1999.雷射與組織的相互作用.雷射生物學報，8（2）：102~108

[3] 張鎮西. 2008. 生物醫學光子學新技術及套用.北京：科學出版社

[4] Ascher P W, Justich E, Schroettner O. 1991. A new surgical but less invasive treatment of central brain tumours. Acta Neurochir, 52:78~80

[5] Boulnois J L. 1986. Photophysical processes in recent medical laser development: a review. Laser in Medical Science, 1:47~66

[6] Graaff R, Koelin M H, de Mul F F M, et al. 1993, Condensed Monte Carlo simulations for the description of light transport. Applied Optics, (32): 426~434

[7] Hale G M, Querry M R, 1973. Optical constants of water in the 200nm to 200wavelength region. Applied Optics, 12:555~563

[8] Niemz M H, Loesel F H, Fischer M, et al. 1994. Surface ablation of corneal tissue using UV, green and IR picosecond laser pulses. Proceeding of SPIE, 2079:131~139

[9] Neimz M H. 2005. 雷射與生物組織的相互作用——原理及套用（第三版）.張鎮西等譯.北京：科學出版社

[10] Parsa P, Jacques S L, Nishioka N S. 1989. Optical properties of rat lver btween 350 and 2200 nm. Applied Optics,28:2318~2324

[11] Wang L H,Jacques S J,1995. Monte Carlo modeling of light transport in multi-layered tissues. University of Texas M D Anderson Cancer Center. Computer methods and Programs in Biomedicine, 47（10）：131~146

[12] Yooh G, Welch A J, Motamedi M, et al. 1987. Development and application of three-dimensional light distribution model for laser irradiated tissue. IEEE Journal of Quantum Electronics, 23(2):1721~1733