離散集

簡介

離散集是拓撲空間的基本概念之一。設 A 為拓撲空間 X 的子集，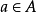

。若存在開集 U 使得

，則稱 a 為 A 的孤立點。與聚點定義對照可知，A 中的點若不是 A 的聚點，則必是 A 的孤立點。自稠密集是不含孤立點點集合。完備集是不含孤立點的閉集。若 A 中每一點都是 A 的孤立點，則稱 A 為 X 中的離散集或孤點集。

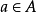
簡單說來，就是對集合中的每個點，都可以畫個圈圈把它和其他點分開來。

比如數軸上的

，其中 0 不是孤點，所以不是離散集合。

在拓撲學中，考慮集合X中的點x，如果x屬於X的子集S，且在X中存在一個x的鄰域，其中不包括S中的其他點，那么x叫做子集S的一個孤點或孤立點。

特別的，在歐幾里得空間（或度量空間）中，考慮集合S及其中的一個點x，如果存在一個包含x的開球，其中不包含S中的其他點，那么x是S的孤點。等價的說，集合S中的一個點x是孤點，若且唯若x不是S的會聚點。

只由孤點構成的集合稱為離散集合。歐幾里得空間的離散子集都是可數的；但是一個可數集合不一定是離散的，比如有理數。參見離散空間。沒有孤點的閉集叫做完美集合（完備集）。

孤點的數目是拓撲不變的，就是說兩個同胚的拓撲空間X和Y有相同數目的孤點。

若一個拓撲空間 X 的子集 A 不包含任何孤立點，稱 A 為自稠的。自稠的閉集稱為完備集。

例如，無理數 B 不是閉集（不是完備的），但是是自稠的。因為任何無理數點的領域至少包含一個其他的無理數點。同時，由於每個有理數點都在其閉包上，所以集合 B 非閉。同理，有理數集是自稠的，但是非閉。