雞爪定理

雞爪定理：三角形一內角的平分線與其外接圓的交點到其它兩頂點的距離及到內心與旁心的距離相等。

雞爪定理指的是設△ABC的內心為I，∠A內的旁心為J，AI的延長線交三角形外接圓於K，則KI=KJ=KB=KC。其中KI、KJ、KB、KC組成的圖形，形似雞爪，故被稱為雞爪定理。

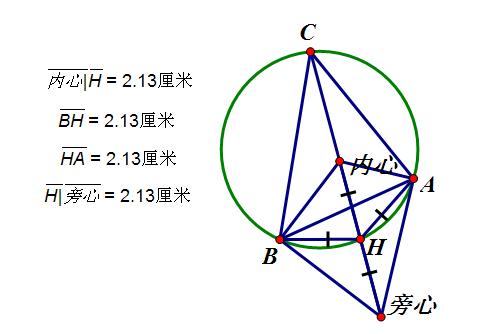
基本介紹

• 中文名：雞爪定理
• 外文名：Chicken theorem
• 性質：定理
• 學科：平面數學
• 套用領域：數學，幾何學
• 特點：四點共圓

證明

1.證明：由內心和旁心的定義可知∠IBC=∠ABC/2，∠JBC=(180°-∠ABC)/2

∴∠IBC+∠JBC=∠ABC/2+90°-∠ABC/2=90°=∠IBJ

同理，∠ICJ=90°

∵∠IBJ+∠ICJ=180°

∴IBJC四點共圓，且IJ為圓的直徑

∵AK平分∠BAC

∴KB=KC（相等的圓周角所對的弦相等）

又∵∠IBK=∠IBC+∠KBC=∠ABC/2+∠KAC=∠ABI+∠BAK=∠KIB

∴KB=KI

∵IBJC四點共圓 且 KB=KI=KC

∴點K是四邊形IBJC的外接圓的圓心（只有圓心滿足與圓周上超過三個以上的點的距離相等）

∴KB=KI=KJ=KC

2.證明：∵E為內心，∴BE平分∠ABC，∴∠2=0.5∠ABC，

∵F為旁心，∴BF平分∠MBC，∴∠CBF=0.5∠MBC

∴∠1+∠CBF=0.5（∠ABC+∠MBC）=0.5×180o=90o，

∴∠EBF=90o，同理：∠ECF=90度，

∴∠EBF+∠ECF=180o， E、B、F、C四點共圓。

∵AD平分∠BAC，且B，D，C三點在△ABC外接圓上，∴DB=DC。①

∵∠6=∠1+∠3，∵∠3=∠4=∠5，∴∠6=∠1+∠5，∵∠1=∠2

∴∠6=∠2+∠5，∴DE=DB。比較①得：DB=DC=DE；

∵E、B、F、C四點共圓，∴D為E、B、F、C四點外接圓的圓心，

∴DB=DC=DE=DF，定理得證。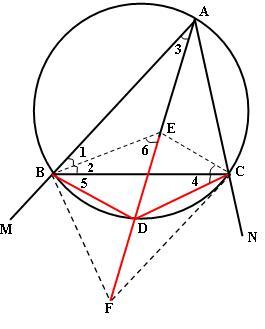

雞爪定理的證明

逆定理

設△ABC中∠BAC的平分線交△ABC的外接圓於K。在AK及延長線上截取KI=KB=KJ，其中I在△ABC的內部，J在△ABC的外部。則點I是△ABC的內心，點J是△ABC的旁心。

證明：利用同一法可輕鬆證明該定理的逆定理。

取△ABC的內心I'和旁心J‘，根據定理有KB=KC=KI'=KJ'

又∵KB=KI=KJ

∴I和I'重合，J和J’重合

即I和J分別是內心和旁心