雙正則理想

雙正則理想(biregular ideal)是一類特殊理想。若環R中元素a所生成的主理想有單位，則a稱為R的雙正則元。環R的一個理想稱為雙正則理想，是指該理想中每個非零元都是雙正則元。雙正則理想是雙正則環。

基本介紹

• 中文名：雙正則理想
• 外文名：biregular ideal
• 領域：數學
• 學科：集合論
• 性質：一類特殊理想
• 特點：雙正則環

概念

雙正則理想(biregular ideal)是一類特殊理想。若環R中元素a所生成的主理想有單位，則a稱為R的雙正則元。環R的一個理想稱為雙正則理想，是指該理想中每個非零元都是雙正則元。雙正則理想是雙正則環。若A是R的雙正則理想，B是A的雙正則理想，則B是R的雙正則理想。環R的雙正則理想的和也是雙正則的，且R含惟一極大雙正則理想，記為B(R)。但至今不知，R/B(R)是否不含雙正則理想。

理想

理想是集合論中的基本概念之一。設S為任意集合，若I⊆P(S)且滿足：

1.∅∈I；

2.若X，Y∈I，則X∪Y∈I；

3.若X，Y⊆S，X∈I，Y⊆X，則Y∈I；

則稱I為集合S上的理想。理想的概念在現代數學的幾乎每個分支中均有套用，且有許多變體或引申。例如，布爾代數上的理想即為集合上的理想的一種變體。設B為任意布爾代數，若B的一個子集I滿足：

1.0∈I，1∉I(其中0，1分別為布爾代數B中的零元與么元)；

2.對任何u∈I，v∈I，有u+v∈I；

3.對任何u，v∈B，若u∈I且v≤u，又v∈I；

則稱I為B上的理想。理想與濾子有非常密切的聯繫。

環

環是對並與差運算封閉的集類，測度論中重要概念之一。設F是Ω上的一個非空集類.如果它對集的並及差運算封閉，即對任何A，B∈F，都有A∪B∈F，A\B∈F，則稱F為Ω上的環。例如，若F是由實直線R上任意有限個左開右閉的有限區間的並集：

的全體構成的集類，則F是R上的一個環.環也是對於交與對稱差運算封閉的集類，並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上，就需要做一系列奠基工作，其中之一是建立一些特殊的集類並研究其性質、環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。

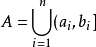
右擬正則理想

右擬正則理想是一類重要的理想。元素的擬正則性是元素冪零性的自然推廣，是從元素刻畫雅各布森根而引入的概念。對環R的一個元a而言，若存在R中元b使得a+b+ab=0(a+b+ba=0)，則稱a為R的右(左)擬正則元，b為a的右(左)擬逆元。環R的一個理想A，若A中每個元都是右(左)擬正則元，則稱A為右(左)擬正則理想。環R的一個右理想稱為右擬正則右理想，若它的每個元皆為右擬正則元。同樣地，可定義左擬正則左理想。任何詣零左(右)理想是左(右)擬正則左(右)理想。有些文獻採用a+b-ab=0(a+b-ba=0)來定義擬正則元。

集合論

數理邏輯四個主要分支之一，是關於無窮集合和超窮數的數學理論。數學裡遇到的無窮有： 無窮過程、無窮小和無窮大。必須能作數學的處理，能進行運算，這樣的無窮才能算作數學的對象。一般說來，集合就是我們把直觀上或思想上的一些確定的彼此不同的對象作為一個整體。組成某一集合的事物(或對象)叫做該集合的元素，用邏輯的話來說就是概念外延相同的全類。構成集合的元素個數為有限時稱為有限集。若構成集合的元素個數為無限多時稱為無限集。德國邏輯學家康托爾於1972年建立。集合論對數學的發展產生了巨大的影響，今天已成為數學各個分支不可缺少的基礎和工具。同時也滲透到數理邏輯的各個分支。