基本介紹
- 中文名:集中不等式
- 外文名:Concentration inequality
- 學科:數學
馬爾可夫不等式,切比雪夫不等式,
馬爾可夫不等式
馬爾可夫不等式給出了一個實值隨機變數取值大於等於某個特定數值的機率的上限。設X是一個隨機變數,a>0為正實數,那么以下不等式成立:
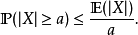
這個不等式可以推廣。對所有的單調嚴格遞增的非零函式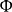 ,都有類似的不等式:
,都有類似的不等式:
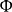
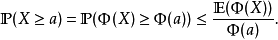
切比雪夫不等式
馬爾可夫不等式給出了隨機變數處於區間 之機率的上限估計。切比雪夫不等式則給出了隨機變數集中在距離其數學期望值距離不超過a的區間上之機率的上限估計。設X是一個隨機變數,a>0為正實數,那么只要對隨機變數
之機率的上限估計。切比雪夫不等式則給出了隨機變數集中在距離其數學期望值距離不超過a的區間上之機率的上限估計。設X是一個隨機變數,a>0為正實數,那么只要對隨機變數 套用馬爾可夫不等式就可以得到:
套用馬爾可夫不等式就可以得到:


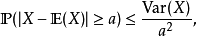
其中的 表示變數X的方差,也就是:
表示變數X的方差,也就是: