隨機對策是一類帶有隨機因素的多步對策。對策論亦稱博弈論,是運籌學的一個重要分支。它所研究的是n(n≥2)個決策者在某種對抗或競爭的局勢下,如何各自作出決策,從而使自己得到自己儘可能最有利的結果。隨機對策是一類帶有隨機因素的多步對策。
基本介紹
- 中文名:隨機對策
- 外文名:stochastic game
- 適用範圍:數理科學
定義









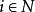


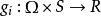



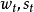

隨機對策是一類帶有隨機因素的多步對策。對策論亦稱博弈論,是運籌學的一個重要分支。它所研究的是n(n≥2)個決策者在某種對抗或競爭的局勢下,如何各自作出決策,從而使自己得到自己儘可能最有利的結果。隨機對策是一類帶有隨機因素的多步對策。









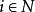


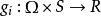



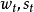
隨機對策是一類帶有隨機因素的多步對策。對策論亦稱博弈論,是運籌學的一個重要分支。它所研究的是n(n≥2)個決策者在某種對抗或競爭的局勢下,如何各自作出決策,...
《隨機微分對策理論與套用》是國防工業出版社於2017年出版的圖書,作者是[美] Kandethody,M.Ramachandran,Chris,P.Tsokos ,由周德雲、方學毅 譯。...
斯塔克爾貝格對策,又稱為主從對策。它是在多級遞階決策系統中,由於決策人所處的地位不同,所形成的一種新的對策形式。由經濟學家斯塔克爾貝格提出。社會現象的結局...
混合對策法是策者不是單一地選擇一個固定的對策,而是按照一定的機率隨機地選用不同的對策,對手也是隨機地選用不同的對策。在許多真實的決策中很難找到一個保守的...
《結構隨機跳變系統理論及其套用》是2007年科學出版社ISBN9787030188168出版的圖書,作者是吳森堂。...
競爭型決策是有關競爭對手之間的決策方法。決策者在競爭場合下作出的決策,或者說競爭的各方為了自己獲勝採取的對付對方的策略,一般稱為對策,研究它的理論和方法,稱...
郭先平教授從事馬爾可夫決策過程(Markov Decision Processes, 簡記為 MDPs)和隨機動態對策的理論和套用研究。其專著《馬爾可夫決策過程》(與侯振挺教授合作)“填補了...
衝突分析(Conflict Analysis)是國外近年來在經典對策論(Game Theory)和偏對策理論(Metagame Theory)基礎上發展起來的一種對衝突行為進行正規分析(Formal Analysis)的...
郭先平教授從事馬爾可夫決策過程(Markov Decision Processes, 簡記為 MDPs)和隨機動態對策的理論和套用研究。其專著《馬爾可夫決策過程》(與侯振挺教授合作)“填補了...
