阿累尼烏斯方程

阿累尼烏斯方程又稱為阿倫尼烏斯方程，是化學動力學的重要公式，由瑞典的阿倫尼烏斯所創立的化學反應速率常數隨溫度變化關係的經驗公式。該公式具有三種不同的表達式，即：指數式、定積分式及微分式。

本方程不僅適用於所有基元反應，而且對於複雜反應中的任一基元反應也是適用的。

基本介紹

• 中文名：阿倫尼烏斯方程
• 外文名：Arrhenius equation
• 又稱：阿龍尼烏斯方程
• 提出者：瑞典化學家阿倫尼烏斯
• 形式：k=A·exp(-Ea/RT)（指數式）

提出

阿倫尼烏斯方程是瑞典化學家阿倫尼烏斯於1889年，總結了大量實驗結果的基礎上，提出的關於化學反應速率常數與溫度之間的關係式。

形式

微分形式

k—溫度T時的反應速度常數，min^-1；

E_a—反應活化能，一般視為與溫度無關的常數，J·mol^-1或·kJ·mol^-1；

T—絕對溫度，K；
R—摩爾氣體常數，8.314J/mol·K。

定積分形式

對微分形式的阿倫尼烏斯方程做不定積分，可得

由上式可以看出，以lnk對1/T作圖應為一條直線，其斜率為-E_a/R。對於大多數化學反應，都有這樣的關係式。若溫度分別為T₁和T₂時，反應速率常數分別為k₁和k₂，則

兩式相減得：

利用換底公式， ，將ln換算成lg得：

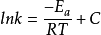
指數形式

阿倫尼烏斯公式還可以引入一個指前因子A(preexponential factor，也稱頻率因子)。

令C=lnA得：

兩邊取指數改寫成：

其中，A—指前因子，也稱為頻率因子或阿倫尼烏斯常數，min^-1；

這個式子表明反應速率常數與溫度呈指數關係。因此，人們將此式稱為反應速率隨溫度而變的指數定律。

適用性

化學反應的類型是比較多的，溫度對反應速率的影響也是相當複雜的，並非所有的化學反應都符合Arrhenius經驗公式。但對於最常見的簡單眼應來說，化學反應速率通常隨溫度的升高而加快，而且成指數關係，可以用Arrhenius公式來定量描述。

本公式雖然最初是從氣相反應中總結出來的，但同樣適用於液相反應和復相催化反應。

另外，本公式不僅適用於基元反應，而且對於複雜反應中的任一基元反應也是適用的。

同時，對於某些複雜反應來說，只要其速率公式滿足 ，（或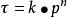 ） 的形式，仍可以運用本公式來描述k與T的關係，只不過此時公式中指數前因子和活化能已不再具有簡單眼應那樣明確的意義，而可能是組成該複雜反應的各個簡單眼應的指前因子或活化能的某種組合。

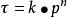
精確性

從定量角度來看，阿氏公式並不是完全精確的。因為公式中關於指數前因子和活化能與溫度無關的假設是不嚴格的， 以致於以lnk對1/T帶作圖所得直線常顯示不同程度的彎曲。

首先， 指前因子A是與溫度有關的。從理論上講， 無論是碰撞理論還是過渡態理論，都推導出A是與T有關的；從實踐來看，用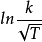(或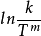) 對條作圖，的確能得到更好的直線。為此不少作者（如Hyne、World和Adams等）從公式的對數式出發進行溫度修正， 使得公式的圖線有了不同程度的改善。

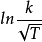
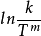
同時， 從活化能的定義來看，由於其來源和物理意義不同，其表達式也各不相同，有的與溫度無關， 有的則與溫度有關。一般地，當把活化能定義為反應物分子間要發生反應所應達到的臨界能量時，這種活化能可以認為是與溫度無關的；而當活化能定義為某個反應發生所需的臨界能量與反應物分子平均能量之差時，這種活化能必定與溫度有關。這是因為臨界能量可能與溫度無關，而分子的平均能量卻與溫度有關。

從上面可以看出，Arrhenius公式中關於A 和E_a與溫度無關的假設是近似的。