阿基米德群牛問題

公元前3世紀下半葉古希臘科學家阿基米德在論著《群牛問題》中記載了本問題。該問題在1880年由阿姆托爾提供了一種解答，該解答需要求解二元二次方程t²-d*u²=1，因d的值達400多萬億，所以完全問題的最小解中牛的總數是一個超過20萬位的數，可見阿基米德當時未必解出過這個問題，且它的結果也與實際不符。歷史上對這個問題的研究豐富了初等數論的內容。

基本介紹

• 中文名：阿基米德群牛問題
• 外文名：The Cattle-Problem
• 提出者：阿基米德
• 提出時間：公元前3世紀下半葉
• 獲解時間：1880年
• 解答者：阿姆托爾
• 適用領域：初等數論

問題的來歷

公元前3世紀下半葉古希臘科學家阿基米德在論著《群牛問題》中記載了本問題。原文用詩句寫成：

朋友，如果你自認為還有幾分聰明，

請來準確無誤地算一算太陽神的牛群，

它們聚集在西西里島，

分成四群悠閒地品嘗青草。

第一群象乳汁一般白潔，

第二群閃耀著烏黑的光澤。

第三群棕黃，

第四群毛色花俏，

每群牛有公有母、有多有少。

先告訴你各群的公牛比例：

白牛數等於棕牛數再加上黑牛數的三分之一又二分之一。

此外，黑牛數為花牛數的四分之一加五分之一，再加上全部棕公牛。

朋友，你還必須牢記花牛數是白牛的六分之一又七分之一，

再搭上全部的棕色公牛。

但是，各群的母牛都有不同的比例：

白色的母牛數等於全部黑色公母牛的三分之一又四分之一。

而黑母牛又是全部花牛的四分之一加上五分之一，

請注意，母牛公牛都要算進去。

同樣的，花母牛的數字是全部棕牛的五分之一加六分之一。

最後，棕色母牛與全部白牛的六分之一加七分之一相一致。

朋友，若你能確切地告訴我這些公牛母牛膘肥體壯、毛色各異，

一共有多少聚集在那裡，

你就不愧為精通算計。

但你還稱不上聰明無比，

除非你能回答如下的問題：

把所有的黑白公牛齊集一起，

恰排成正方形，整整齊齊。

遼闊的西西里島草地，

還有不少公牛在聚集。

當棕色的公牛與花公牛走到一起，

排成一個三角形狀。

棕色公牛、花公牛頭頭在場，

其他的牛沒有一頭敢往裡闖。

朋友，你若能夠根據上述條件，

準確說出各種牛的數量，

那你就是勝利者，

你的聲譽將如日月永放光芒。

題目: 西西里島的草地上， 太陽神的牛群中有公牛也有母牛，公牛母牛都是白、 黑、 花、 棕4種毛色； 白色公牛多於棕色公牛， 多出的頭數是黑色公牛的 12+13 ； 黑色公牛多於棕色公牛， 多出的頭數是花公牛的 14+15 ； 花公牛多於棕色公牛， 多出的頭數是白色公牛的 16+17 ； 白色母牛是黑牛的 13+14 ； 黑色母牛是花牛的 14+15 ；花母牛是棕色牛的 15+16 ； 棕色母牛是白色牛的 16+17 .問各色公牛與母牛有多少頭？

問題的深意

阿基米德的論文向來是以命題的形式來表達的，而這篇的體例不同，它是用詩句寫成的。標題是給埃拉托塞尼的信。胡爾奇(Hultsch)曾猜想這是阿基米德“顯本領(tour de force)”之作，以此向亞歷山大的學者們(特別是阿波羅尼奧斯)挑戰。但它的真實性頗值得懷疑，因為“群牛問題”大概很早以前就已存在，阿基米德只是重新研究而已，詩句也未必出自他的手。

問題的敘述

詩的大意是：西西里島草原上有一大群牛，公牛和母牛各有4種顏色。設W、X、Y、Z分別表示白、黑、黃、花色的公牛數， w、x、y、z分別表示這白、黑、黃、花色的母牛數。

要求有

，

，

，

，

，

，

，

為一個正方形（數），

為一個三角形（數）（即形如 的數，m為正整數）。

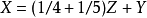
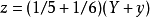
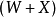
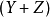
求各種顏色牛的數目。

倒數第二個條件中的正方形數有兩種解釋：

一種是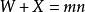 ，因為要擠成一個正方形，還需要考慮身長與體寬的比，故右端不是任意兩個正整數之積mn而是 （k是常數），稱為“較簡問題”。

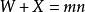
另一種為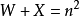 （完全平方數），即長與寬上牛的數目相等，稱為“完全問題”。

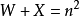
問題的解決

“較簡問題”已由武爾姆解決。“完全問題”在1880年為阿姆托爾(Amthor)所解決。

即使較簡問題，牛的總數也已達到頭之多！

而完全需要求解二元二次方程 。

最小解牛的總數是，位數超過20萬！當時阿基米德未必解得出來。

而即使沒有最後兩個條件，群牛問題的最小正數解也達50'389'082，故它的敘述自然與實際不符——西西里島再大也裝不下這么多牛的。但歷史上對這個問題的研究豐富了初等數論的內容。