在數學中,阿佩爾序列是得名於十九世紀法國數學家保羅·埃米爾·阿佩爾(Paul Émile Appell)的一類多項式序列。
基本介紹
- 中文名:阿佩爾序列
- 外文名:Appell sequence
- 分類:數理科學
定義,等價的阿佩爾序列定義方式,遞歸公式,參見,
定義
阿佩爾序列滿足以下關係:
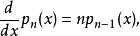
等價的阿佩爾序列定義方式
最常見的阿佩爾序列的定義就是以上的
對所有的n= 1, 2, 3, ...,
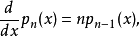
並且p0(x) 是一個非零常數
的關係式。此外,以下的條件也可以被驗證是與之等價的:
純數數列 {cn}n=0,1,2,...滿足c0≠0,並且
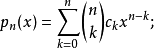
純數數列 {cn}n=0,1,2,...滿足c0≠0,並且

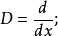
對所有的n= 0, 1, 2, ...,
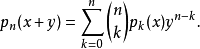
遞歸公式
假設
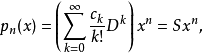
其中後一個等式是在以x為不定元的多項式構成的線性空間中的線性運算元S的定義式。並定義:
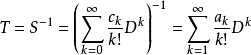
為S的逆運算元,其中的係數ak是形式冪級數的逆係數。這樣得到
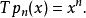

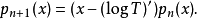
參見
- 謝弗序列
- 影子演算
- 廣義阿佩爾多項式
- Wick積
