閾元件

閾元件是一種類型的門，它的命名是根據元件的輸出取決於輸入變數的權和內部閾值相比較而得來的。輸入變數為1時的加權和與內部閾值相比較，當加權和等於或大於該閾值時，輸出為1，而當它小於閾值時，輸出為0。

基本介紹

• 中文名：閾元件
• 外文名：Threshold element
• 所屬範圍：邏輯門
• 功能：邏輯網路的數學控制
• 套用學科：物理等
• 適用領域：電路、邏輯等

數學表達式

從數學上來看，閾元件的邏輯關係可以表示為：

式中 表示輸入變數， 表示當 時，對 所加的權，T是閾值。 和 是實數， 是二值變數，運算是代數運算。

由單個閾元件實現的開關表達式的形式，和其他各類門有所不同，它們不是固定不變的。這是因為改變閾值或權值可以實現許多不同的函式。正是由於這種靈活性，使閾門成為一個極為有用的邏輯部件，它能經濟地實現許多開關函式。

方框圖符號

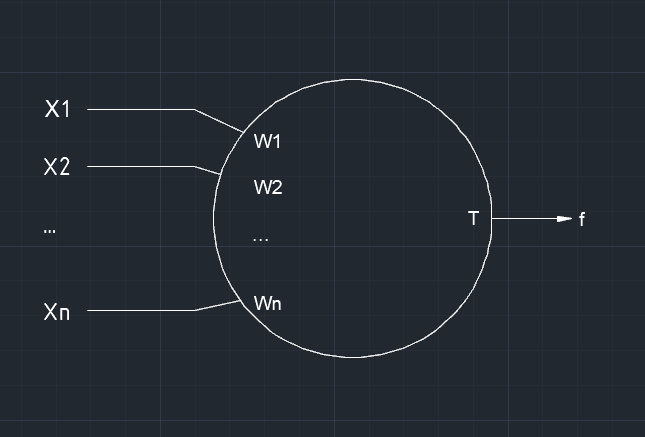
閾元件的方框圖符號見圖1所示

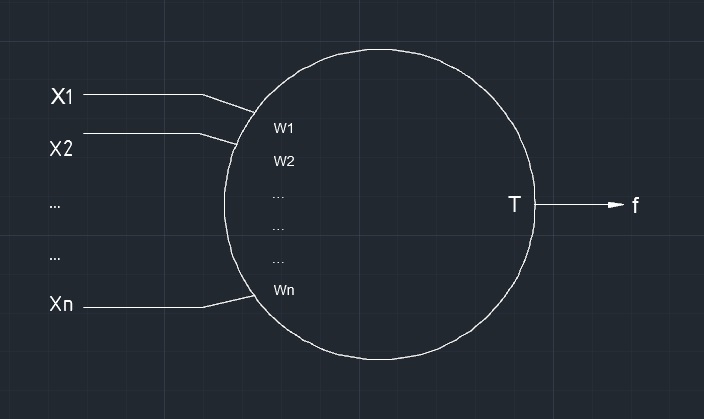
圖1閾元件方框圖

閾函式

可由單個閾元件實現的開關函式叫做1—可實現的，或者叫做閾函式。研究這些函式，已經做了很多工作。雖然能夠用單個閾元件實現許多開關函式，然而，實現大多數函式還是要用較多的閾元件。

邏輯關係

根據已知的閾元件確定閾函式，是簡單的。反過來，由閾函式確定閾元件卻不容易。因為閾元件的輸出由每種可能的輸入狀態唯一確定，所以由已知閾元件所實現的函式也是唯一的。在舉例研究之前，用如下稍有不同的樣式重新描述閾元件的邏輯關係數學表達式

式中 ，閾元件有 個輸入，和 關聯的輸入是通常所說的偏置輸入，它是等於1的常數。在這個不等式中，包括閾輸入在內的 個輸入的集合，可表示成權閾矢量 。因此這個不等式提供了一個簡潔的符號，用這種形式的不等式會更為方便一些。現在研究一個有權閾函式 的閾元件。如果我們研究全部輸入組合，並求出相應的和 ，它們用表格表示出來：

從而求出了特徵數和函式的典型形式 。這個函式的簡化形式為 ，這就是通常所說的多數函式，多數函式是能用單個閾元件實現的幾個對稱函式中的一個。

不等式相容性

綜合閾元件實現已知函式的問題，在於尋求一個權閾矢量，這個權閾矢量滿足函式規定的 個不等式。甚至不等式有解存在時，一般說來，這也不是一個容易的問題。是不是有解存在，取決於 個不等式組的相容性。如果不等式是不相容的，則不存在滿足全部不等式的權閾矢量；如果不等式是相容的，則求得的不等式的解是一組權閾矢量或是1—可實現的。為了說明問題，現研究函式 ，列出不等式組 ，如下表所示

不等式可寫成如下樣式：

從而求得如下關係：

這些關係說明了不等式是相容的，因此，它是有解的。各個權的順序關係必須有如下的次序：

應該是一個解，很顯然沒有唯一解，因為將這個解乘上大於1的任何正數，得到的結果也是不等式的另一個解。通常規定閾函式實現時，採用整數權，而且讓它的絕對值的和 是最小的 。因為整數便於計算，權的絕對值的和最小則有利於經濟而穩定地實現函式。

線性可分性

由前述可知，閾函式是以線性可分性為其特徵的——不等式組能分為兩個相容群，一個群中各個不等式等於或大於零，而另一群中的各個不等式小於零。非線性可分函式的例子是 ，由如下不相容的不等式群可證明它是非線性可分的：

線性可分性的幾何結構是一個n維的超立方體，這個立方體的 個頂點表示 個輸入組合。通過在各個頂點指定1或0值來定義函式，若且唯若1值頂點和0值頂點能用一個超平面分開時，開關函式是1—可實現的。因為一個線性定義一個平面，所以函式是線性可分的。如圖2所示是兩個畫在三維方體上的函式，一個是線性可分的，另一個則不是。在圖2中a，函式 是線性可分的，因為一個垂直螢幕且包含了虛線的平面，能把1值頂點和0值頂點分開。在圖2中b，函式不是線性可分的，因為無法畫出一個平面穿過方體，把1值頂點和0值頂點分開。一個函式的1值頂點像這樣隔開，並且按對角線配置時，這函式叫做違反了平行四邊形法則。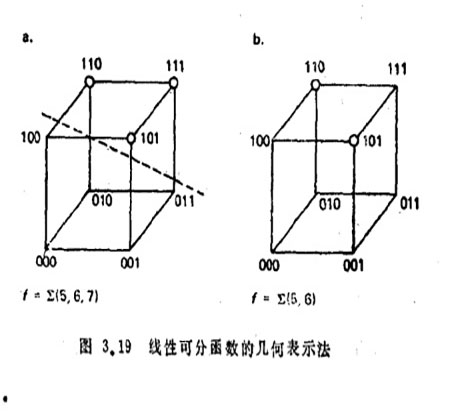

圖2

可調邏輯網路

閾值邏輯是一種其每個閾元件中包含更多信息的邏輯系統，它作為神經功能的模擬量被提出來，其名稱是根據“閾元件的輸出取決於輸入變數的權於內部閾值相比較”而得來的。閾元件特別適合於“可調邏輯”網路，可調邏輯網路的調節作用是由簡單的數字控制得到的。例如，我們研究三個輸入的元件的閾值電平改變效應。權閾矢量 實現函式 ，如果閾值增加1，則此元件的權閾矢量為 ，它實現的函式是 ；如果閾值再增加1，則此元件實現的函式是 。所能得到的函式，取決於輸入權。

邏輯網路的數學控制性能在諸如計算機設計、信息檢測、圖像識別等領域中有著重要的意義。計算機的處理器是由邏輯門構成的網路，這些邏輯門之間由互相傳送信號的通路相連線。這些信號總是二進制的。就是說，每個信號明確指出0和1這兩種可能性中的一個。每個門有一個或多個輸入和一個輸出，某個門的輸入通常是其它門的輸出，或者是來自外圍設備的信號。同樣，一個門的輸出可以作為其它門的輸入，或者送到傳送裝置以將信息傳送到外界。