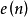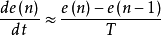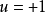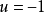基本介紹
開關曲線是使時間最優控制函式改變符號的曲線。二階時間最優控制系統的狀態空間是二維歐幾里得平面
(或是
中包含原點為內點的某區域
),對於控制作用是標量的情況,如果一條通過坐標原點的曲線
把相平面
分為兩部分
和
(或把
分為兩部分
和
),即
(或
),使得在
(或
)內最優控制取正值,在
(或
)內最優控制取負值,在曲線
上,最優控制的取值亦是完全確定的,並且經過原點的那段
必定是時間最優軌線,則稱曲線
是時間
最優控制系統的
開關曲線。當控制作用是二維向量時,時間最優控制系統有兩條開關曲線。這樣,二階線性定常受控系統的時間最優控制的綜合在於求得其開關曲線。
Bang-Bang控制的開關曲線
Bang-Bang控制介紹
Bang-Bang控制又叫
開關控制或快速控制。實質上是最優控制的一種特殊形式——
時間最優控制。常規的PID反饋系統,通常是以被控變數的最大超調量,偏差的積分面積等等作為評定控制品質的指標,而Bang-Bang控制則是被控變數從一個狀態到另一個狀態的時間最短為其品質指標。系統設計的核心問題是設計
開關函式。根據開關函式及系統的狀態,決定控制作用是正向作用還是反向作用。它雖然可以看成是一種位式調節,但顯然與一般位式調節有明顯不同,是因為它引進了時間最優的概念,它的切換不僅受調節偏差控制,而且受偏差的微分信號控制,因而可以避免位式控制超調量大的弊病。另外,開關控制還有一個穩定的工作點,即當
及
均為零,執行機構不動作。
開關曲線分析
舉例說明如下:已知對象特性曲線為
控制作用的不等式約束為:
,實際上執行機構以
與
兩位(開關)控制。
設計步驟如下:
圖1表示了
與
的兩簇曲線,通常稱通過坐標原點的曲線
為開關曲線。
 圖1 開關曲線
圖1 開關曲線控制要求是系統在某一初始狀態P點,在開關作用下,經最短時間回到零點(即
)而穩定下來。由圖2知,不論初始狀態如何,最終必然要轉移到開關曲線
上,然後再沿開關曲線回到原點,若初始狀態在
上(如P點),則系統控制作用保持
,直到達到OM曲線為止,開關才變換方向,使控制作用變為
並一直保持到平衡點。當初始狀態在
之下(如P’點)系統的控制作用一直保持為
,直到ON曲線為止,開關才變換方向使控制作用變為
,並一直保持到終點。可見,在對象為二階系統時,開關作用的符號只改變一次,一般而言,若對象為n階要實現最優控制,開關作用將至多切換
次,顯然,此時若想如二階系統那樣確定改變控制作用的轉換曲線(開關曲線)就不那么簡單。因為要確定n維狀態空間中轉曲面(開關曲面)就困難。更何況確定了轉換曲面後,還得研究狀態軌跡,並確定切換點(或切換時間)。
 圖2(a) 二階系統的相平面圖
圖2(a) 二階系統的相平面圖 圖2(b) 二階系統的時域回響圖
圖2(b) 二階系統的時域回響圖比較圖3(a)、(b)中
軌跡與
軌跡,可以看出
軌跡時間最短。
從實際觀點出發,為簡化算法,我們可以用一直線方程近似地表示拋物線開關曲線,這時所得到的系統就不再是最佳的,但它是很接近於最佳系統的。
 圖3 說明最短與非最短的相平面圖(a)
圖3 說明最短與非最短的相平面圖(a) 圖3 說明最短與非最短的相平面圖(b)
圖3 說明最短與非最短的相平面圖(b)開關控制系統每計算調節一次,都需要檢測控制偏差
,並計算其微分,
,判斷系統狀態是在開關曲線上方、下方或處於開關曲線上,若在開關曲線上方,則實行
的控制;若在開關曲線的下方,則實行
的控制;若在原點上,則
。每次動作後狀態軌跡與開關曲線相交,立即改變控制方向。根據上述解釋可作出Bang-Bang控制程式框圖,圖略。


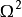
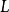

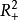
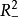
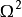
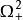
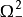
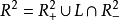
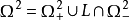
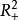
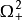
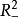
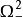
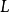
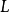
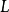
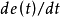
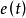
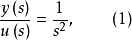
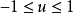
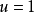
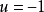
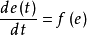

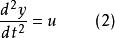
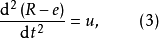
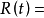
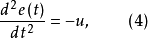
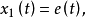
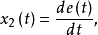
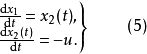
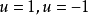
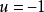
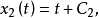

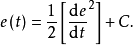
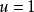
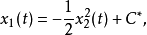
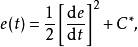
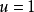
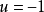
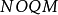
 圖1 開關曲線
圖1 開關曲線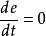
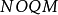
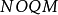
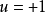
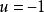
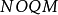
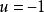
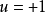
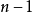
 圖2(a) 二階系統的相平面圖
圖2(a) 二階系統的相平面圖 圖2(b) 二階系統的時域回響圖
圖2(b) 二階系統的時域回響圖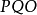
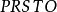
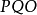
 圖3 說明最短與非最短的相平面圖(a)
圖3 說明最短與非最短的相平面圖(a) 圖3 說明最短與非最短的相平面圖(b)
圖3 說明最短與非最短的相平面圖(b)