閉系統定律(law of a closed system)亦稱豪伯定律、閉語句定理,數學中的重要定理,即對於構成一個閉系統的n個命題:如Ai成立則Bi(i=1,2,…,n)成立,則當Bi成立時Ai(i=1,2,…,n)也成立。
基本介紹
- 中文名:閉系統定律
- 外文名:law of a closed system
- 別稱:豪伯定律、閉語句定理
- 所屬學科:邏輯學
- 相關概念:閉系統,逆命題
基本介紹
閉系統定律的證明

舉例分析



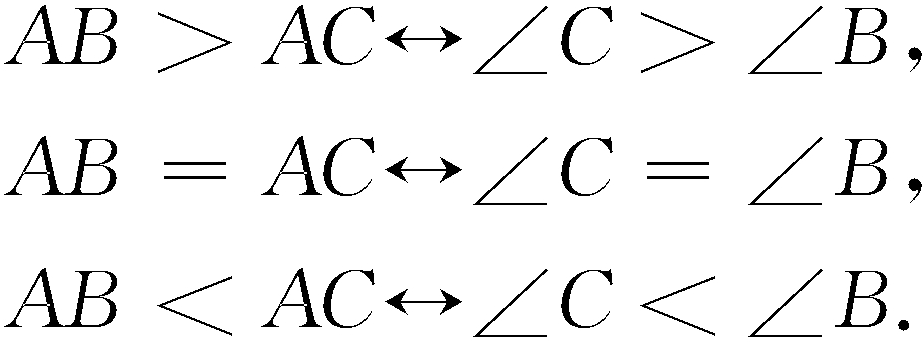



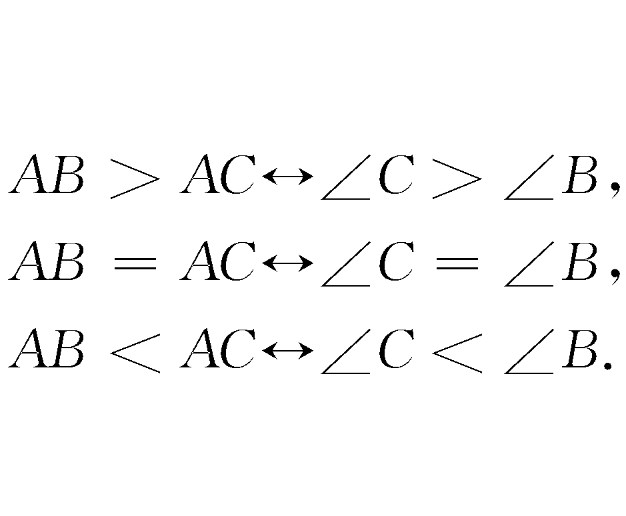
閉系統定律(law of a closed system)亦稱豪伯定律、閉語句定理,數學中的重要定理,即對於構成一個閉系統的n個命題:如Ai成立則Bi(i=1,2,…,n)成立,則當Bi成立時Ai(i=1,2,…,n)也成立。




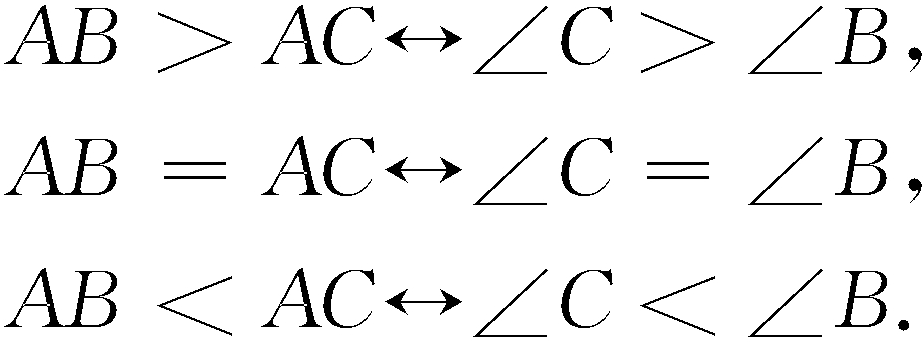



閉系統定律(law of a closed system)亦稱豪伯定律、閉語句定理,數學中的重要定理,即對於構成一個閉系統的n個命題:如Ai成立則Bi(i=1,2,…,n)成立,則當Bi...
閉系統是一類特殊的支命題系統,指分斷式命題的構造模式,分斷式命題是一種複合命題,判定某類數學命題真假時使用的一種命題形式。...
控制系統分為開環控制系統和閉環控制系統。事物定律的核心是道法自然。道:泛指事物的規律和人們共同生活所遵循的行為準則和規範。法:是反映統治階級意志,由國家制定...
1 簡介 2 閉口系熱力學第一定律 閉口系統簡介 編輯 閉口系統是指沒有和外界發生物質交換的熱力學系統,有時又稱為控制質量系統。閉口系統的質量保持恆定,取系統時...
注意:是質心,而不是重心,因為除非重力場是均勻的,否則同一物質(系統)的質心與重心通常不在同一假想點上。巴普斯定律套用 編輯 巴普斯定律巴普斯定理1的套用一 ...
熱力學第一定律的能量方程式就是系統變化過程中的能量平衡方程式, 是分析狀態變化過程的根本方程式。它可以從系統在狀態變化過程中各項能量的變化和它們的總量守恆這一...
西蒙認為,組織就是作為決策的個人所組成的系統。決策貫徹於管理的全過程,管理就...那么我們如果把這個現象切入上面的這條定律,可以說對於一個企業的興衰起決定作用...
卡斯柯定律,聞名於國內信號領域的卡斯柯,成立於1986年,是鐵路系統第一家中外合資企業。它與上海捷運的淵源,始於上世紀90年代。...
