研究長度測量，保證量值準確和測量單位統一的技術。
基本介紹
- 中文名：長度計量技術
- 技術：長度計量技術
正文,簡史,測量方法,單項測量和綜合測量,絕對測量和相對測量,接觸測量和不接觸測量,直接測量和間接測量,主動測量和被動測量,測量誤差,系統誤差,隨機誤差,粗大誤差,測量結果的數據處理,相關書籍,
正文
研究長度測量，保證量值準確和測量單位統一的技術。長度計量中的長度包括距離、角度、表面粗糙度、圓度和直線度等以"米"為基本單位的幾何量，所以長度計量也常稱為幾何量計量。長度測量是將被測長度與已知長度比較，以確定被測長度量值的過程。量值以數字和單位表示，例如用遊標卡尺（見卡尺）測量圓柱體直徑,測得的數值20.24毫米就是量值。
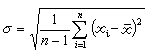長度計量技術
長度計量技術主尺上的刻度就是已知長度。機械製造中進行長度計量是為了保證工件的互換性和產品質量，一般以毫米和微米作為測量單位。長度計量的主要內容是研究和建立長度計量基準、實現長度計量的量值傳遞、研究孔徑測量、角度測量、直線度測量、平面度測量、表面粗糙度測量、圓度測量、圓柱度測量、螺紋測量、齒輪測量、自動測量等方法和測量誤差，以及測量結果的數據處理等。
簡史
古代，人類為了測量田地等就已經進行長度測量。最初是以人的手、足等作為長度單位。但手、足大小不一,在商品交換中遇到了困難,於是便出現了以物體作為測量單位,如公元前2400年出現的古埃及腕尺,中國商朝 (公元前16～前11世紀)出現的象牙尺和公元9年製造的新莽銅卡尺。長度單位經歷了多次演變，1496年和1760年英國先後採用端面和線紋的碼基準尺作為長度基準。1789年法國提出建立米制，1799年製成阿希夫米尺(見長度計量基準)。在機械製造業中最早套用的是機械原理的測長技術。1631年發明游標細分原理。18世紀中葉，人們已套用螺紋放大原理進行長度測量。機械測長技術迄今仍是工業測量中的基本測量技術之一。
它能達到很高的精確度，例如利用精密螺紋副測長和多齒分度技術測角可分別達到 2微米/1000毫米和0.1″/360°的精確度。套用光學原理的測長技術也出現較早。19世紀末出現立式測長儀（見測長機），20世紀20年代前後已套用自準直、望遠鏡、顯微鏡和光波干涉等原理測長，使工業測量進入不接觸測量領域，解決了一些小型複雜形狀工件，例如螺紋的幾何參數、樣板的輪廓尺寸和大型工件的直線度、同軸度等形狀和位置誤差的測量問題。套用光波干涉原理使現代測長精確度達到了0.01～0.02微米/100 毫米。
長度計量技術
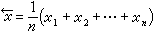長度計量技術氣動原理的測長技術是在20年代後期發展起來的。它的測量效率高,對環境條件要求不高,適宜在車間使用，但其示值範圍小，阻礙了它的發展。套用電學原理測長是在30年代初期發展起來的。首先出現的是套用電感原理的測微儀（見比較儀）。後來由於電子技術的發展，電學原理的測長技術發展很快。它可以把微小誤差放大到100萬倍,也就是說0.01微米的誤差值可以10毫米的刻度間隔表示出來。電子線路並能實現各種演算和自動測量。60年代中期以後，在工業測量中逐步套用電子計算機技術。電子計算機具有自動修正誤差、自動控制和高速數據處理的功能，為高精度、自動化和高效率測量開闢了新的途徑，因而在長度測量中套用得越來越廣泛。現代測量技術已經發展成為精密機械、光、電和電子計算機等技術相結合的綜合性技術。
測量方法
在工業測量中，要根據被測對象的材質、形狀、大小、批量和精度等選定可能的和符合經濟原則的測量方法。
單項測量和綜合測量
單項測量是分別測量被測件的幾何參數，例如螺紋的中徑、半角和螺距；齒輪的齒形、周節和齒向等，可根據測量結果分析工藝誤差。綜合測量是測量由各有關參數折合而成的某一當量或綜合測量各有關參數，例如用螺紋量規檢驗螺紋折合中徑和齒輪單面嚙合檢查儀測量齒輪切向綜合誤差等。綜合測量是一種模擬實際使用情況的測量方法，測量結果能較真實地反映使用質量，測量效率也高，適用於檢驗工件合格與否。
絕對測量和相對測量
接觸測量和不接觸測量
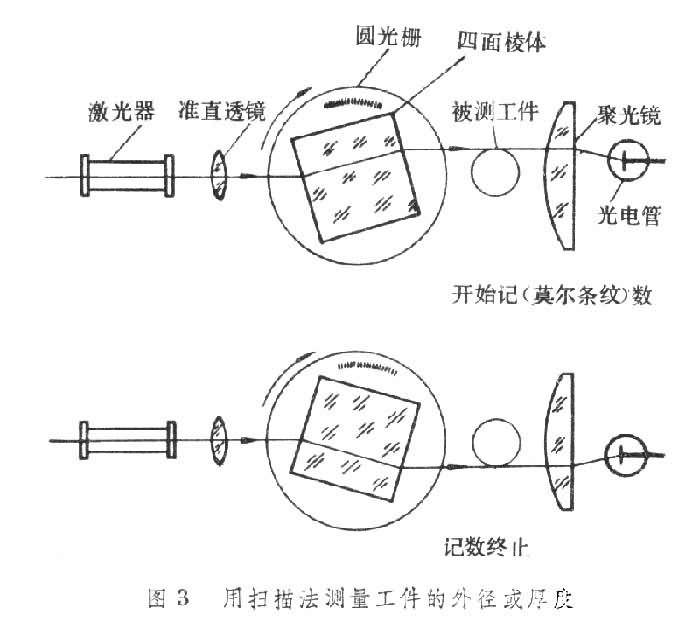
接觸測量是指被測表面與長度測量工具的測頭有機械接觸；不接觸測量是指利用光學、氣動等瞄準定位方法，長度測量工具的瞄準定位部分或測頭等不與被測表面接觸,例如用雷射掃描法(見雷射測長技術)測量外徑和氣動測頭測量直徑等。
直接測量和間接測量
直接測量是將被測長度與已知長度直接比較，從而得出所需的測量結果，是常用的測量方法。間接測量的測量結果是通過測量與被測長度有一定函式關係的長度，經過計算後才得到的，例如測量大型工件外徑時，也有採用測量圓周長度，經過計算後求出外徑的。
長度計量技術
長度計量技術主動測量和被動測量
主動測量是把加工過程中測量所得信息直接用於控制加工過程以得到合格工件的測量。被動測量也稱線外測量，是測量結果不直接用於控制加工精度的測量。
測量誤差
測量結果與被測長度真值之間的差。真值是理論上的概念，一般說來是不知道的，但可以認為保存在國際計量局或各國國家計量中的"米"基準，按定義規定在特定條件下的值為真值 1米。在工業測量中，常用實際值或修正過的算術平均值來代替真值。實際值是滿足規定精確度的量值。測量誤差的表示方式有兩種：
①以量值表示，即以所測得量值與實際值之差表示，以這種方式表示的誤差稱為絕對誤差；
②以比值表示，即以絕對誤差與實際值之比表示，以這種方式表示的誤差稱為相對誤差，例如用雷射干涉儀測長時，如其最大相對誤差為10-7，則表示在規定條件下，測量1米長度的誤差應不大於0.1微米。 測量誤差按其基本性質可分系統誤差、隨機誤差和粗大誤差。
系統誤差
由於偏離規定工作條件或由測量方法引起的、按規律變化的誤差。它包括:已知長度本身不準確引起的誤差,例如線紋尺的線距誤差;測量機構的原理誤差;溫度變化引起的誤差;不正確安裝引起的誤差，例如圓光柵安裝偏心等。一般說來，系統誤差可以計算或測量出來,是一種有可能修正的誤差。以正確度(correct-ness)表示其大小。
隨機誤差
也稱偶然誤差。這是一類在實際條件下多次測量同一長度時，誤差的絕對值和符號以不可預定方式變化的誤差。隨機誤差是由一些不易確定的因素，例如配合間隙、彈性變形、摩擦力等引起的，以精密度(precision)表示其大小。
粗大誤差
在規定條件下超出預期的誤差，這類誤差是不計入測量結果中去的。
測量結果與被測長度真值的一致程度以精確度(ac-curacy)或準確度表示。它是正確度和精密度的綜合,通常簡稱為精度。若已修正系統誤差，則精確度常用不確定度來表示。不確定度 (uncentainty)表示由於存在測量誤差而對所測量值不能肯定的程度，以標準偏差表示其大小。
測量結果的數據處理
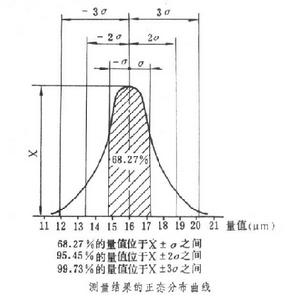
在測量所得數據中已消除了粗大誤差，只含系統誤差和隨機誤差。對系統誤差一般是針對每一可能產生誤差的來源採取不同的處理措施，例如用雷射干涉儀測長時，須按測量環境的溫度、濕度和氣壓的變化對波長作修正計算以提高測量精確度。對於隨機誤差,可運用機率論和統計學中的方法來處理,以減少其對測量結果的影響並估計出最終殘留影響的大小。測量中，常把多次測量被測長度後所得不盡一致的數據x1、x2、...xn取算術平均值作為測量結果。根據機率論的大數定律,只要測量次數n足夠多，就可以提高精密度。測量過程中隨機誤差的出現基本上是遵循常態分配規律的。以標準偏差 σ（也稱均方根誤差）表示量值分散的程度,。σ越小，表示大誤差出現的機率越小,精密度越高。按常態分配機率計算(見圖)，單次測量誤差小於±σ的機率為68.27%，即每測量三次其中就有一次出現測量誤差大於 ±σ的可能，而單次測量誤差小於 ±2σ和±3σ的機率分別為95.45%和99.73%。因此±2σ和±3σ常用於表示測量結果的可信程度。
長度計量技術
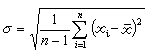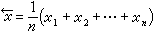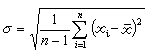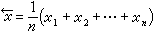長度計量技術