長幅圓內旋輪線

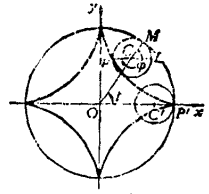
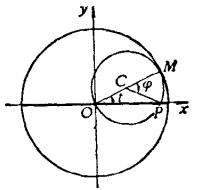
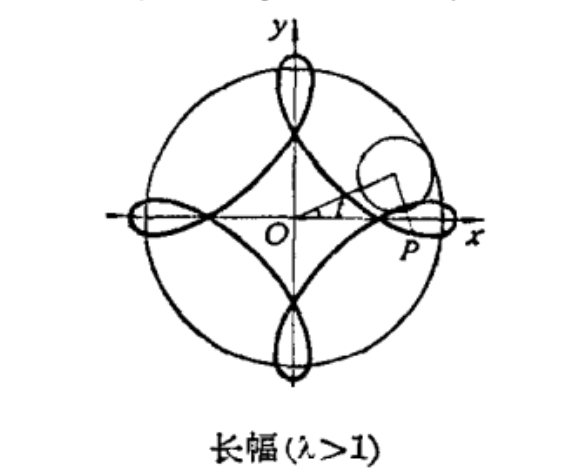
長幅圓內旋輪線和短幅圓內旋輪線統稱內次擺線，又稱變幅內擺線，是內擺線的一種，是平面上半徑為r的動圓Q(稱為母圓)在半徑為R的定圓O(稱為基圓)內部無滑動地滾動時，固定在圓Q平面內的點M的軌跡。設點M到動圓心的距離為l，此旋輪線的參數方程為：x=(R-r)cosφ+lcos(R/r-l)φ;y=(R-r)sinφ-lsin(R/r-l)φ,其中(R>r)，當l>r時為長幅圓內旋輪線；當l<r時為短幅圓內旋輪線；當R=2r時為橢圓。

基本介紹

• 中文名：長幅圓內旋輪線
• 所屬學科：數學
• 所屬問題：平面解析幾何
• 簡介：圓內旋輪線的一種

基本介紹

圓內旋輪線 長幅圓內旋輪線是圓內旋輪線的一種，圓內旋輪線是一動圓沿一定圓內部滾動而無滑動時，圓周上一點M的軌跡，或叫內擺線。

圓內旋輪線的參數方程是

其中a是定圓半徑，b為動圓半徑，是動圓圓心和定圓圓心連線與X軸的夾角。

圓內旋輪線的形狀由m=a/b的值決定(如圖1～圖4)。

特殊地，當m=4時，曲線有4支，叫做星形線，其方程為

或(如圖3)。

圓內旋輪線也叫內擺線。

長(短)幅圓內旋輪線一動圓沿一定圓內部滾動而無滑動時，圓外一點M(圓內一點N)的軌跡叫做長(短)幅圓內旋輪線。

長(短)幅圓內旋輪線的參數方程是

其中a為定圓半徑，b為動圓半徑，。是動圓外(內)一點M(N)到動圓心的距離，λ>1為長幅圓的內旋輪線(如圖5)，0<λ。

特殊地，當a=2b時，長(短)幅圓內旋輪線是橢圓。

長(短)幅圓內旋輪線統稱為內次擺線。

例題解析

一定圓O，半徑為R，一動圓C，半徑為r(R>r)，當動圓與定圓內切而滾動時，試求動圓上一定點P的軌跡。

圖7

解 取點P在兩圓相切的切點P'時的動圓位置為初始位置(圖7)，以初始位置的兩圓連心線為x軸，O為原點，建立直角坐標系．設動圓經過某一時刻後，圓心在C。令OC'繞點O轉到OC位置時轉過的角為t,小圓的半徑C'P’繞圓心轉到CP位置時轉過的角為φ,則，

其中

用m代替R/r，得

其中t為參數，r是動圓半徑，m是定圓與動圓的半徑之比。

圖8

說明 當m=2時，軌跡方程為故軌跡是定圓位於x軸上的直徑(圖8)．

當m=4時，軌跡方程為

此軌跡稱為四尖內旋輪線，也稱星形線(圖7)，

當m為任意值時，軌跡稱為圓內旋輪線或內擺線．如點P位於動圓半徑上，到動圓圓心的距離為λr，當λ>1時，軌跡稱為長幅圓內旋輪線；當0<λ<1時，軌跡稱為短幅圓內旋輪線。