n個有序的元素應有n!個不同的排列，如若一個排列使得所有的元素不在原來的位置上，則稱這個排列為錯排；有的叫重排。
如，1 2的錯排是唯一的，即2 1。1 2 3的錯排有31 2，2 3 1。這二者可以看作是1 2錯排，3分別與1、2換位而得的。
基本介紹
- 中文名：錯排問題
- 外文名：Derangement
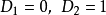
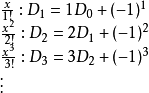
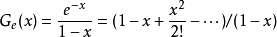
基本信息,錯排公式,遞歸關係,通項公式求解,錯排生成算法,性能分析,原始碼,
基本信息
錯排問題是組合數學發展史上的一個重要問題，錯排數也是一項重要的數。令
是
的一個錯排，如果每個元素都不在其對應下標的位置上，即
，那么這種排列稱為錯位排列，或錯排、重排（Derangement）。
我們從分析1 2 3 4的錯排開始：
1 2 3 4的錯排有:
4 3 2 1，4 1 2 3，4 3 1 2，
3 4 1 2，3 4 2 1，2 4 1 3，
2 1 4 3，3 1 4 2，2 3 4 1。
第一列是4分別與123互換位置，其餘兩個元素錯排。
1 2 3 4->4 3 2 1，
1 2 3 4->3 4 1 2，
1 2 3 4-> 2 1 4 3
第2列是4分別與312（123的一個錯排）的每一個數互換
3 1 2 4->4 1 2 3，
3 1 2 4->3 4 2 1，
3 1 2 4->3 1 4 2
第三列則是由另一個錯排231和4換位而得到
2 3 1 4->4 3 1 2，
2 3 1 4->2 4 1 3，
2 3 1 4->2 3 4 1
上面的分析結果，實際上是給出一種產生錯排的結果。
錯排公式
遞歸關係
為求其遞推關係，分兩步走：
第一步，考慮第n個元素，把它放在某一個位置，比如位置k，一共有n-1种放法；
第二步，考慮第k個元素，這時有兩種情況：（1）把它放到位置n，那么對於除n以外的n-1個元素，由於第k個元素放到了位置n，所以剩下n-2個元素的錯排即可，有
种放法；（2）第k個元素不放到位置n，這時對於這n-1個元素的錯排，有
种放法。
根據乘法和加法法則，綜上得到
特殊地，
。此外，存在
因此，
。
通項公式求解
下面利用遞推關係證明通項公式，可利用母函式方法，也可利用容斥原理。首先基於母函式方法進行證明，令
有遞推關係得
因此
，
，
而1/（1-x）可以替換成無窮級數（無窮遞縮等比數列）
故（由對應次數項係數相等）
此外，也可基於容斥原理進行證明。設
為數i在第i為上的全體排列，
。則有
故每個元素都不在原來的位置上的排列數為
錯排生成算法
上面對錯排公式進行了證明，在實際套用中，為得到所有合理的錯排方案，當n較大時，手動枚舉費時費力，需要程式依照算法生成所有錯排方案。因此下面分別研究了遞歸法、基於字典序的篩選法和改進字典序法的算法思想、流程和程式實現。
遞歸法
遞歸法的思想為逐位安排：首先安排第一位，並記錄被安排的數，然後遞歸，同樣的方法安排第二位……直到安排到到第n位。若第n位滿足錯排，則錯排方案數加一，並輸出該錯排，並返回；否則直接返回，返回後，撤銷該位安排的數。其中，安排每一位時，都遍歷了n個數，下一位的遞歸返回後都撤銷這位安排的數，然後遍歷到下一個數，重新遞歸。這樣通過不斷遍歷和遞歸，實現了所有錯排方案的生成。算法偽代碼如下：
為了更清晰地描述算法，下圖給出算法流程，其中Rec(x)為安排第x位的遞歸函式。
基於字典序的篩選法
基於字典序的篩選法的思想非常簡單，即首先按照字典序生成每一個排列，然後檢驗生成的該排列是否滿足錯排，如果是則方案數加一併輸出，否則生成下一個排列。算法流程如下圖所示。
改進字典序法
改進字典序法是在字典序的基礎上改進而成，主要思想是：按照字典序，一旦出現不滿足錯排的排列，則由此開始跳過接下來的不滿足錯排的一些排列。由於避免了長段的非錯排的排除流程，因此相對傳統字典序法能夠提高算法效率。算法流程如下圖所示。
圖中，i表示安排第i位，Flag表示不滿足錯排的元素的位置，均滿足則默認為n+1。藍色方框表示根據字典序找下一個排列，並記錄其不滿足錯排的Flag。紅色方框表示根據算法規則跳過接下來的不滿足錯排的一些排列，然後尋找關鍵位置，給此位置安排滿足錯排的數。藍色方框部分只需根據字典序生成下一個排列，並記錄最左側不滿足錯排的元素位置為Flag即可，具體流程不再贅述。下面給出錯排的一個引理，然後給出紅色方框的算法流程。
引理1：給定一個不滿足錯排的排列P1，在全排列的字典序中的下一個排列記為P2，在錯排的字典序中的下一個排列記為P3。設P1中不滿足錯排的最左側的元素下標為i，P1和P2從左側開始比較第一個不相等的元素的下標記為j，P1與P3從最左側開始比較第一個不相等的元素的下標記為k，則一定有k≤min{i, j}。
例如：錯排P1=23541，則P2=P3=24135，i=4，j=k=2，成立。
再如：錯排P1=42513，則P2=42531，P3=43152，j=k=2，i=4，成立。
引理1的證明很簡單，j即為根據字典序法從右往左找到的第一個下降的位置。如果i<j，說明錯排的位置在j的前面，此時調整j及其後面的元素位置得到的排列仍然不滿足錯排，而應該調整i及其後面的元素位置，此時k=i。如果i >j，說明錯排的位置在j的後面，此時調整j及其後面的元素位置得到的排列就改變了原先不滿足錯排的元素位置，因此新排列可能滿足錯排，此時k≤j，因此得證。
根據引理1，紅色方框的算法流程為：
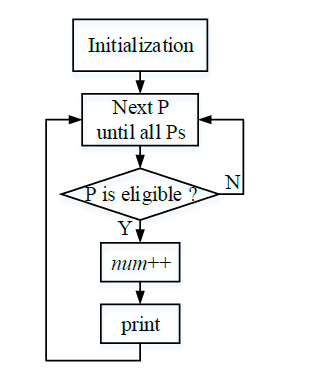
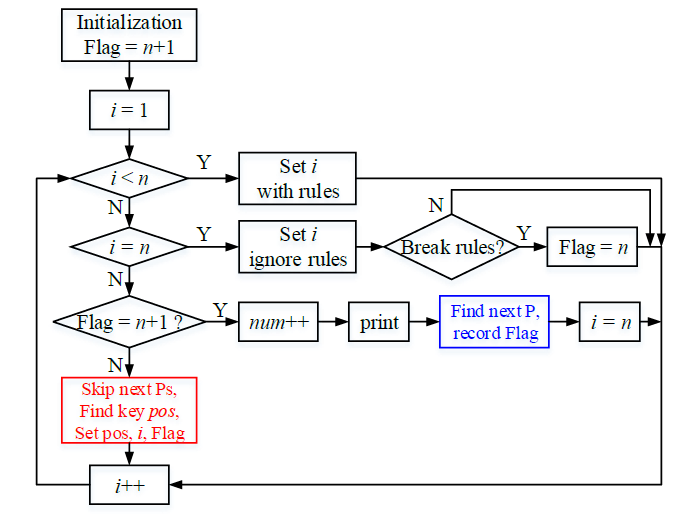
- 從右往左找下降，找到下降位置為pos；如果pos>Flag，則pos=Flag，並清空pos及其後所有位置的元素；
- 對該排列的第pos個元素，從原先的取值開始往上加。對於某一新的取值，如果滿足錯排，則將其記為pos的元素，設定i=pos，重置Flag=n+1並退出；否則，從該位置起重新進入1)，即繼續往前找下降的位置。
為了更清晰地說明算法流程，以n=5為例給出以下結果：
- 前4個循環形成了2143，均滿足錯排規則；第5個循環中，只剩下數字5，不得不安排到第5個位置上，形成了21435，破壞了規則，Flag=5；
- 下一個循環i=6，Flag=5，進入紅色方框，下降的位置為4，小於Flag，所以pos取4，清空pos及其後位置上的3、5；pos位置從3開始往上加，加到5，滿足錯排，設定pos的元素為5，i=4，Flag=6；
- 下一個循環i=5，設定末尾元素為3，滿足規則，i=5，Flag=6；
- 下一個循環i=6，Flag=5+1表明滿足錯排，num++，輸出第一個錯排21453；然後按照字典序找到下一個排列21534，滿足錯排，Flag=6，設定i=5；
- 下一個循環i=6，Flag=5+1表明滿足錯排，num++，輸出第二個錯排21534；然後按照字典序找到下一個排列21543，不滿足錯排，記錄Flag=4，設定i=5；
- 下一個循環i=6，Flag=4，進入紅色方框，如上算法得到pos=2，設定pos的元素為3，i=2，Flag=6；
- 接下來三個循環設定末尾三位為1、5、4；i=5，Flag=6；
- ……
根據上述分析及舉例可見，改進字典序法相對基於字典序的篩選法有以下優點：
- 至少從不滿足錯排的位置和下降的位置兩者之左開始進行調整，從而跳過了不必要的循環。
- 設定關鍵位置的元素後，其後元素（除末尾）的設定依然按照錯排規則進行，因此也跳過了不滿足錯排的排列。
- 依然沿用了字典序法中找下一個排列的方法，用以快速尋找滿足錯排的下一個排列，越到最後，該排列越可能滿足錯排，所以採用了直接生成再判斷的方法，而沒有採用逐元判斷生成的方法。
為保證算法可延續性，末尾元素的設定忽略了錯排規則，生成後再判斷，否則算法可能會無法繼續，如n=5時算法起始21435的生成。
遍曆法
文獻[2]給出一種常數時間的錯排生成算法，其本質屬於遍曆法，下面以n=5為例說明其算法：
第一步：將最後一位數移至第一位，其餘的數順次向後移動，產生錯排d。
如：12345→51234。
第二步：考察d的第二個位置，除去第一個位置的數和2不能放在這個位置上，其餘均可。
如：51234→51234或53214或54231。
考察d的第三個位置，除去第一、第二個位置上的數和3不能放在這個位置上，其餘的數都可以。
如：51234→51234→51234或51432
51234→53214→53214或53124或53412
51234→54231→54231或54132
以此類推，n個數的錯排一直考察到第n個位置為止，結束第二步。
第三步：重複第一、第二步的過程，循環這個程式。
如：12345→51234→45123→34512→23451。
這個循環過程直到第一步產生234⋯(n-1)(n)1，繼續執行第二、三步，然後結束。
在算法實現上，生成每一個排列採用無循環處理，時間複雜度為O(1)，因此生成所有錯排的時間複雜度為
。
性能分析
上面詳述了四種算法思想和流程，下面給出各算法的複雜度分析和性能比較。
對於遞歸法，n個元素的錯排方案數為
，每個錯排均需遍歷到，因此基本複雜度為
。遞歸函式其中有n次循環，若不考慮錯排規則，則每次循環均調用遞歸函式，考慮錯排規則時調用次數滿足
，因此
。但由於遞歸函式的調用開銷是很大的，系統要為每次函式調用分配存儲空間，並將調用點壓棧予以記錄。而在函式調用結束後，還要釋放空間，彈棧恢復斷點。所以，考慮函式處理過程，整體看來，遞歸法的效率並不高。
對於基於字典序的篩選法，字典序法的複雜度為
，對每個排列檢驗其是否為錯排的複雜度為
，因此該算法的時間複雜度為
。
對於改進字典序法，由於其相對基於字典序的篩選法的優點，所以複雜度必然會降低。由於算法中邏輯判斷與處理很多，分析其複雜度非常困難。但由於其跳過了大部分的非錯排，因此複雜度大約為
。因此，改進字典序法和文獻[2]提出的方法的複雜度大體相同。
綜合上述分析可見，算法總體效率大致為：改進字典序法≈文獻[2]方法>基於字典序的篩選法>遞歸法。下面根據數值實驗結果給出各算法的性能比較。
表 各算法運行耗時比較（單位：ms）
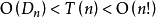
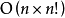
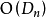
算法 | n=9 | n=10 | n=11 | n=12 | n=13 |
改進字典序法 | 5 | 44 | 468 | 5534 | 69704 |
文獻[2]方法 | 5 | 51 | 553 | 6552 | 83087 |
篩選法 | 8 | 84 | 1050 | 13553 | 181979 |
遞歸法 | 21 | 186 | 2067 | 25243 | 334661 |
表1給出了各算法運行耗時比較，圖4給出了運行時間隨n變化的對數曲線圖。從上述結果可知，改進字典序法和文獻[2]方法的性能相當，前者稍好一些。這兩種算法的運行耗時大約為基於字典序的篩選法的一半，而篩選法的運行耗時大約為遞歸法的一半。注意：由於所取n值在10附近，且曲線縱坐標取log10(t)，因此所得結果大致為直線，只能說明n取10左右時，曲線局部為近似直線，並不說明整體都成此特性。總之，數值實驗分析結果與上述時間複雜度分析結果一致。此外，改進字典序法具有最好的算法性能。
原始碼
遞歸實現
void Recursion(int x){ if (x > n) { num_r++; for (int i = 1; i <= n; i++)//輸出每一個錯排 printf("%d ",dearr_r[i]); printf("\n"); return; } for (int i = 1; i <= n; i++) { if (occup_r[i] == 0 && x != i) //x指安排第x個位置 { occup_r[i] = 1; //vis[i]記錄i是否已經被安排 dearr_r[x] = i; Recursion(x + 1); occup_r[i] = 0; //回退，撤銷安排的i } }}基於字典序實現
int LexiOrder(int n){ int num_l = 0; bool Flag = true; int *seq = new int[n]; for (int i = 0; i < n; i++) seq[i] = i + 1; num_l++; for (int i = 0; i < n; i++) { if (seq[i] == i + 1) { num_l--; Flag = false; break; } } if (Flag) { for (int i = 0; i < n; i++)//輸出每一個錯排 printf("%d ",seq[i]); printf("\n"); } for (int i = n - 2; i >= 0;) { if (seq[i] < seq[i+1]) { for (int j = n - 1;j >= 0; j--) { if (seq[j] > seq[i]) { int tmp = seq[i]; seq[i] = seq[j]; seq[j] = tmp; for (int k1 = i + 1, k2 = n - 1; k1 < k2; k1++, k2--) { int tmp = seq[k1]; seq[k1] = seq[k2]; seq[k2] = tmp; } num_l++; Flag = true; for (int i = 0; i < n; i++) { if (seq[i] == i + 1) { num_l--; Flag = false; break; } } if (Flag) { for (int i = 0; i < n; i++)//輸出每一個錯排 printf("%d ",seq[i]); printf("\n"); } i = n - 2; //重新從右邊開始 break; } } } else i--; } delete []seq; return num_l;}改進字典序法實現
int AdLxOrder(int n){ int num_a = 0; int *dearr = new int[n + 1]; int *occup = new int[n + 1]; int Flag = n + 1; //記錄不滿足錯排的元素位置，均滿足則為n+1 for (int i = 0; i <= n; i++){ dearr[i] = 0;occup[i] = 0;} for (int i = 1, len = 0; i <= n + 1; i++) { if (i < n) //安排第i個位置 { for (int j = 1; j <= n; j++) //安排第i個位置 { if (occup[j] == 0 && j != i) { occup[j] = 1; //occup[j]記錄j是否已經被安排 dearr[i] = j; //安排dearr[i] break; } } } else if (i == n) //安排最後一位 { for (int j = 1; j <= n; j++) //安排第i個位置，無論是否滿足 { if (occup[j] == 0) { occup[j] = 1; //occup[j]記錄j是否已經被安排 dearr[i] = j; if (j == i) Flag = n; break; } } } else //i == n+1 { if (Flag == n + 1) //滿足，輸出，並找字典序下一個 { num_a++; for(int k = 1;k <= n; k++) printf("%d ",dearr[k]); printf("\n"); int pos = 0; for (int k = n; k > 1; k--) //從右往左找下降 { if (dearr[k - 1] < dearr[k]) { pos = k - 1; for (int m = n; m > pos; m--) { if (dearr[m] > dearr[pos]) //找到後綴中較大的最小元素 { if (dearr[m] == pos) Flag = pos; //記錄不滿足的位置 int tmp = dearr[m]; //交換 dearr[m] = dearr[pos]; dearr[pos] = tmp; //記錄不滿足的位置（只記錄最左側） for (int k1 = pos+1, k2 = n; k1 < k2; k1++, k2--) { if (dearr[k1] == k2 && Flag > k2) Flag = k2; //記錄不滿足的位置 if (dearr[k2] == k1 && Flag > k1) Flag = k1; //記錄不滿足的位置 int tmp = dearr[k2]; //陸續交換 dearr[k2] = dearr[k1]; dearr[k1] = tmp; } i = n; //循環末尾有i++，此處特取n break; } } break; } } } else //找關鍵位置的下一個值 { //關鍵位置：下降位置和不滿足位置的最左者 int pos = 0; for (int k = n; k > 1; k--) //從右往左找下降 { if (dearr[k - 1] < dearr[k]) { pos = k - 1; if (pos > Flag) //pos取下降位置和不滿足位置的最左者 pos = Flag; for (int m = pos; m <= n; m++) occup[dearr[m]] = 0; //全部重置 for (int m = dearr[pos] + 1; m <= n; m++) //從dearr[pos]+1開始找 { if (occup[m] == 0 && m != pos) //給pos找到下一個值 { dearr[pos] = m; occup[m] = 1; i = pos; Flag = n + 1; break; } } if (Flag == n + 1) break; else k = pos + 1; //重新向前找下降，循環末尾有k--，此處特+1 } } } } } delete []dearr; delete []occup; return num_a;}