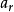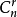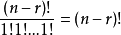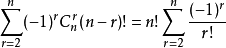全錯位排列被著名數學家歐拉(Leonhard Euler,1707-1783)稱為“組合數論的一個妙題”的“裝錯信封問題”的兩個特例。
基本介紹
- 中文名:全錯位排列
- 外文名:All dislocation arrangement
- 提出者:歐拉
- 又稱:“裝錯信封問題”
- 領域:數學
簡介,基本簡介,公式證明,研究錯排問題的方法,枚舉法,遞推數列法,多項式模擬,
簡介
基本簡介
一個人寫了n封不同的信及相應的n個不同的信封,他把這n封信都裝錯了信封,問都裝錯信封的裝法有多少種?
公式證明
n個相異的元素排成一排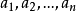 。則
。則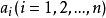 不在第i位的排列數為:
不在第i位的排列數為:
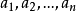
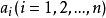
證明:
設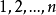 的全排列
的全排列 的集合為I,而使
的集合為I,而使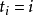 的全排列的集合記為
的全排列的集合記為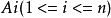 ,
,
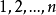

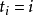
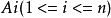
則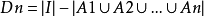 .
.
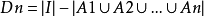
所以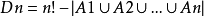 .
.
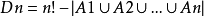
注意到 。
。

由容斥原理:
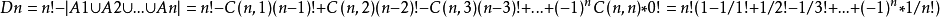
研究錯排問題的方法
枚舉法
對於情況較少的排列,可以使用枚舉法。
- 當n=1時,全排列只有一種,不是錯排,D1= 0。
- 當n=2時,全排列有兩種,即1、2和2、1,後者是錯排,D2= 1。
- 當n=3時,全排列有六種,即1、2、3;1、3、2;2、1、3;2、3、1;3、1、2;3、2、1,其中只有有3、1、2和2、3、1是錯排,D3=2。用同樣的方法可以知道D4=9。
- 最小的幾個錯排數是:D1= 0,D2= 1,D3=2,D4= 9,D5= 44,D6= 265,D7= 1854.
遞推數列法
對於排列數較多的情況,難以採用枚舉法。這時可以用遞歸思想推導錯排數的遞迴關係式。
顯然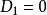 ,
,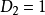 。當
。當 時,不妨設n排在了第k位,其中k≠n,也就是
時,不妨設n排在了第k位,其中k≠n,也就是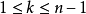 。那么考慮第n位的情況。
。那么考慮第n位的情況。
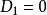
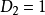

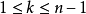
- 當k排在第n位時,除了n和k以外還有n-2個數,其錯排數為Dn-2。
- 當k不排在第n位時,那么將第n位重新考慮成一個新的“第k位”,這時的包括k在內的剩下n-1個數的每一種錯排,都等價於只有n-1個數時的錯排(只是其中的第k位會換成第n位)。其錯排數為Dn-1。
所以當n排在第k位時共有Dn-2+Dn-1種錯排方法,又k有從1到n-1共n-1種取法,我們可以得到:
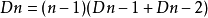
在上面我們得到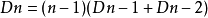 從這個公式中我們可以推出Dn的通項公式,方法如下:
從這個公式中我們可以推出Dn的通項公式,方法如下:
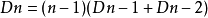
為書寫方便,記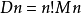 ,則
,則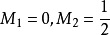
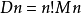
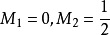
當n大於等於3時,由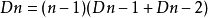 ,即
,即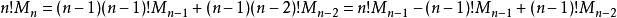 。 所以,
。 所以,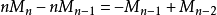 。
。
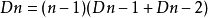
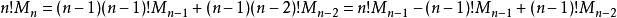
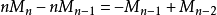
於是有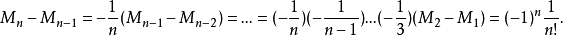
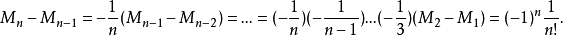
將上面式子分邊累加,得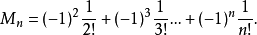
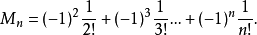
因此,我們得到錯排公式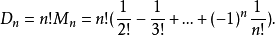
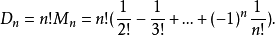
多項式模擬
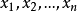
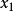
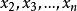
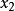
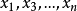
記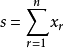 ,錯排結果為
,錯排結果為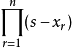 中
中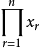 的係數
的係數
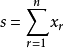
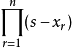
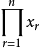
記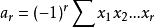 為基本對稱多項式,
為基本對稱多項式,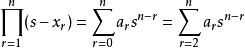
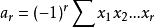
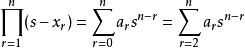
從 選出
選出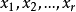 ,然後從
,然後從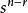 選出
選出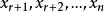 ,組成
,組成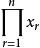

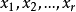
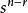
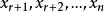
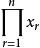
從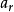 選出r個x有
選出r個x有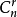 種可能,從
種可能,從 選出其餘的n-r個x有
選出其餘的n-r個x有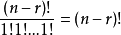 種可能
種可能