研究來源 空氣動力學 所包含的內容非常廣泛,最初推動這一學科發展的巨大動力,來源於20世紀初人們想要飛的願望。從那時起大規模的航空航天研究,以及對具有內流的機械(如
噴氣發動機 、泵和渦輪機)所開展的研究與改進,一直在豐富著空氣動力學。此外,30多年來,空氣動力學在土木工程中的套用也取得新的進展,這類問題涉及的是自然風,所以主要局限於低速、不可壓縮的流動現象。在套用中,空氣動力學還與氣象學緊密結合,特別是近地大氣邊界層的湍流流動。由於大多數工程結構對風表現為鈍體形狀,所以風工程的研究重點是鈍體空氣動力學。
簡介 鈍體是相對於流線體而言的,流線體是前圓後尖、表面光滑、略像水滴的形狀。具有這種形狀的物體在流體中運動時,流體沿物體的輪廓流動,基本不產生分離和尾流,因而受到的阻力最小。而對於鈍體,即非流線體,在其邊界上會形成流動分離,後部會產生寬闊的尾流,並伴有旋渦脫落現象(可能是周期性或非周期性)。鈍體空氣動力學源自於流體力學,因此其運動描述方法和控制方程與流體力學是一致的。
鈍體繞流現象 邊界層與流動分離 在正常氣壓和氣溫下,空氣的黏性很小,儘管如此,黏性對於空氣流動的影響仍十分顯著,特別是在靠近物體表面的區域。由於空氣的黏性效應,與物體表面接觸的空氣貼附在物體表面,它將減慢靠近物體表面的一層空氣的運動,這一空氣層就稱為
邊界層 。與大氣邊界層中的平均風剖面類似,在邊界層內,氣流的速度從物體表面上為零(即無滑動)逐漸增大到邊界層外的氣流速度。實際上,大氣邊界層就是一個典型的物體邊界層例子。邊界層是空氣黏性效應的一個重要表現。
圖1 如果邊界層內的流體微粒速度因慣性力減小到使靠近物體表面的氣流倒流,便出現了邊界層分離。這種減速效應是因為氣流中存在
逆壓梯度 ,當這種逆壓梯度很大時,就會引起流動分離,例如鈍體拐角的繞流就能產生這樣大的逆壓梯度。分離層形成離散的旋渦,並脫落到鈍體後方的氣流中(圖1),這些旋渦使得分離點(如拐角或房檐等)附近出現非常大的吸力。
雷諾數效應 由於空氣具有質量,根據
牛頓第二定律 (或N-S方程),空氣除了具有黏性力外還具有慣性作用,即氣流中影響最大的兩個作用是黏性和慣性作用,它們的相互關係成為確定可能出現哪種類型流動特性或現象的判據,這個判據可表示為無量綱參數,即雷諾數Re,它代表了流體內的慣性力與黏性力之比。對於表面特徵尺寸為 L 的某一體積氣流,作用在其微團上的黏性應力可由邊界層內的速度變化梯度來確定,可近似表示為μU/L,其中μ是空氣的黏性係數,根據Bernoulli方程,對於速度為U的流體,慣性力近似用ρU
2 。來表示,這裡ρ為空氣密度。於是雷諾數可表示為
其中ν=μ/ρ為空氣的分子運動黏性係數(簡稱動黏性係數),表征了由層流流體各層之間的分子運動所引起黏性力的大小。Re較大時,慣性效應起主要作用,反之則黏性效應起主要作用。
下面以圓柱體為例說明雷諾數對鈍體繞流的影響。如圖2所示,在層流流場中,隨著雷諾數從低逐漸變高,圓柱體繞流會出現多種不同的流動形態。當雷諾數很低時(Re≈1),流體將對稱地附著在整個圓周上(圖2(a))。當Re≈20時,繞流形態仍是對稱的,但在背風側出現了流動分離,並形成一對始終停留在圓柱體背風側表面附近的大旋渦(圖2(b))。
圖2 當30≤Re≤5×10
3 時,旋渦將在圓柱體兩側交替脫落,並在下游形成一條清晰穩定、交錯排列的“渦跡”或“渦街”(圖2(c)),這些交錯排列的旋渦以略低於周圍流體的速度向下游移動。由於該現象最早由馮·卡門(Von Karman)發現並解,因此被稱為
卡門渦街 。在這一雷諾數範圍內,除了旋渦本身外,圓柱體後的尾流是比較平滑而規則的,流動雖然是非定常的,但基本上可認為是層流。當雷諾數繼續升高到5×10
3 <Re≤3×10
5 範圍內時,規則的卡門渦街消失,分離點上游的附著流仍是層流,但在分離點處可觀察到三維流動;尾流由層流向湍流過渡,隨著雷諾數的升高,分離點也逐步向上游移動,尾流的寬度逐步增加,尾流中層流向湍流的過渡部位從離圓柱較遠的下游處逐步靠近圓柱體表面,尾流的紊亂程度也逐步增加。當雷諾數接近臨界點(約3×10
5 )時,分離點位於圓柱兩側的邊緣(圖2(d)中的A和B兩點),此時尾流寬度相當大,超過了圓柱體的直徑,而旋渦的脫落仍是有規律的。
當
雷諾數 超過臨界點(約3×10
5 )後,流動分離點突然遷移到下游(從圖2(d)中的A和B兩點分別遷移到從圖2(e)中的A’和B’兩點),使得尾流變窄(因而阻力下降),同時旋渦的脫落也變得相當隨機而無規律。3×10
5 ~5×10
5 雷諾數範圍對應了圓柱表面邊界層(附著流)內發生層流向湍流過渡的狀態。當雷諾數超過約3.5×10
5 後,雖然尾流仍然十分紊亂,旋渦脫落又變得頗有規律。
鈍體尾流的雙重小波包分解研究 根據湍流相干結構和非相干結構不相關的特性,提出了一種鈍體尾流雙重小波包分解的新算法,將湍流的運動分解成相干分量和非相干分量。該算法以湍流相干分量和非相干分量的相關係數作為疊代的控制指標,減小了過去算法中的隨意性。用該算法對大長寬比的鈍體尾流三維超音波流速儀測量數據的分析表明:1.鈍體間距與寬度之比大於4時,鈍體間的相互影響可以忽略不計;2.流線型的鈍體尾流紊動強度較小。
研究概述 鈍體尾流最顯著的特點是繞流體後緣旋渦的周期性脫落,形成卡門渦街。受卡門渦街的影響,繞流體表面的壓力也會發生周期性變化,當繞流體表面壓力變化頻率與繞流體的固有頻率接近時,會發生共振,從而引起繞流體的破壞,在水利工程中,常見的如電站尤其是抽水蓄能電站攔污柵的破壞。因此,研究鈍體尾流的形成機理、結構特徵有十分重要的工程套用價值。從流動特點來看,卡門渦街是湍流中一種典型的相干結構,對這類流動的深入分析既可深化人們對湍流的認識,又有利於湍流模型的發展。
Hussain在20世紀80年代對湍流中的相干結構進行了全面的評述,並提出了湍流場的雙重分解(即將湍流分量分解成相干分量和內稟分量)和三重分解(將湍流物理量分解成時均分量、相干分量和內稟分量)。在試驗研究中,過去普遍採用條件採樣技術和相平均方法提取湍流中的相干結構。隨著小波分析的發展,小波分析已成為湍流相干結構分析的一個極其重要的工具。Siegel和Weiss採用小波包算法提取和分析湍流的渦量結構和特徵,Chainais等根據相干結構內壓力的變化特性,用小波變換研究了旋渦流動中的湍流間歇特性和相干結構,Li提出了一種小波相關分析方法並用其研究了剪下湍流的相干結構,李櫟等用小波分析研究了平壁湍流猝發現象。
該研究提出了一種分析鈍體尾流的雙重小波分解算法,並深入分析了鈍體前後緣對鈍體尾跡流特性的影響。
研究結論 該研究提出了一種提取鈍體尾流相干運動的小波包分解疊代算法,並引入一無量綱參數,即湍流相干分量與非相干分量間的相關參數,作為疊代的控制指標,從而減小了分解算法的隨意性。該方法可以推廣套用於其它類型湍流的多尺度分析及湍流特性分析。
針對電站攔污柵尾流特性,用該算法分析了5種柱體尾流實驗數據,結果表明:1)當柵葉間距與柵葉寬度之比大於4時,柵葉間的相互影響可以忽略不計;2)流線型柵葉尾流的紊動強度很小,在攔污柵設計時應優先採用。
 圖1
圖1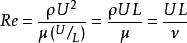
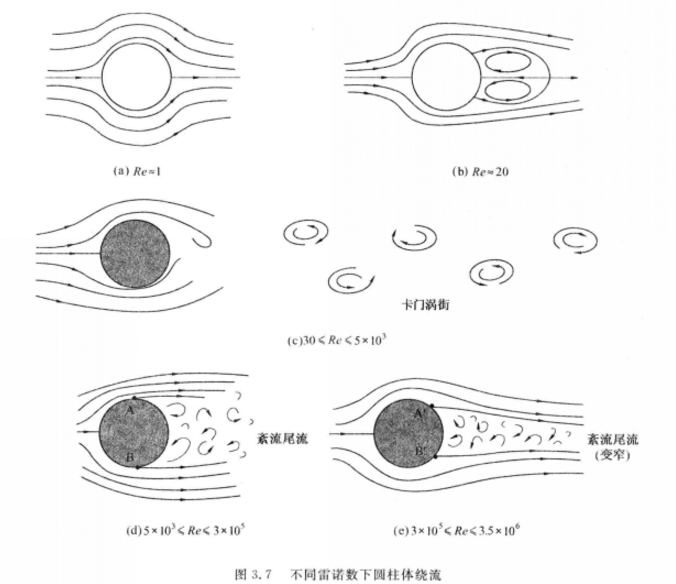 圖2
圖2
 圖1
圖1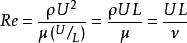
 圖2
圖2