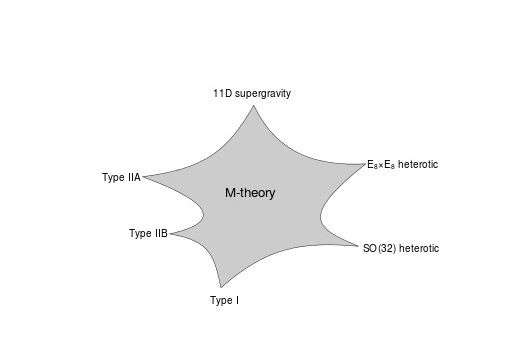
藉助一條歧管，把一系列數論重大問題與物理學結合起來。
基本介紹
- 中文名：重大數論問題聯合表示m理論
- 所屬學科：數學物理
- 套用：套用於廣義相對論和量子力學融合的m理論
原理,費馬大定理的岐管就是m理論岐管,1、計算岐管中的線段需要黎曼猜想,2、與歐拉公式聯繫起來,黎曼猜想是二階邏輯問題,基本特點,
原理
藉助一具歧管，將一系列重大數學問題與物理學廣義相對論和量子力學的m理論聯繫起來。
起因
1，從四色定理開始
法蘭西斯·古德里於1831年生於倫敦，在1852年提出的猜想，只需要四種顏色為地圖著色。這是因為他發現在平面上或者球面上，只能有4個區域兩兩相連，英國數學家德摩根證明了平面上不存在5個區域兩兩相連。
1974年德國的林格和美國的楊斯證明了在曲面上染色定理，例如，在一個汽車輪胎形狀的環面需要7種顏色，因為可以構造7個兩兩相連的區域，6種顏色肯定不夠的；在有兩個洞的雙環面需要8種顏色，因為可以構造8個兩兩相連的區域，7種顏色肯定不夠的；...。
2，可以構造無窮多個兩兩相連區域
如果一般人不能理解，慢慢道來：現在有兩根管子，一個記為1，一個記為2，它們代表兩個區域。假定所有的管子都是可以隨意拉伸和彎曲的。把兩根管子端端相連，就是一個汽車輪胎一樣的環，它有兩個區域，我們再用一根直管子記為3，安在這個環的中間，一頭連著區域1，一頭連著區域2，現在它是有兩個洞的雙環了，有三個區域兩兩相連。
現在用一個“丁”字型的三叉管，記為區域4，三個連線埠分別與區域1，區域2，區域3相連。於是現在有4個區域兩兩相連；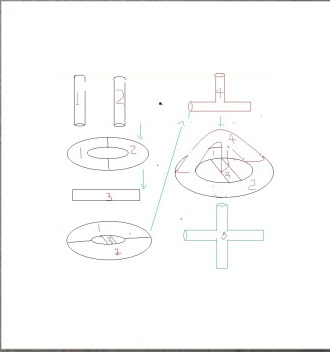
4個區域兩兩相連
再用一根四叉管記為區域5，有4個連線埠分別與區域1，2，3，4區域相連，現在有5個區域兩兩相連。
這個步驟可以無限制進行下去，用五叉管，六叉管，。.。構造無窮多個區域，它們都是兩兩相連的。
把歧管兩兩相連之間給定距離可以等價轉換成為貨郎擔問題（p=np問題）。
3，圖論與數論聯繫起來
數學家和物理學家把這個叫做岐管。
區域1，代表第一個素數2;；第二個區域代表第二個素數3；....；第n個區域代表第n個素數。
在數論中，最重要的元素就是素數，歐幾里得證明了有無窮多個素數，並且它們有一個特點就是兩兩互素。無窮多個兩兩互素的素數與無窮多個兩兩相連區域 一 一對應。
圖論與數論聯繫起來了。將不同的學科分支聯繫起來的思想叫做朗蘭茲綱領。
把這個圖8中的岐管倒過來，就像一個網子，籃球網子。籃球網子是把籃球往裡面投。
岐管或者稱為篩子
4，篩子
公元前300年古希臘有一個數學家叫做埃拉特斯特尼，他把這個網子當成篩子，把自然數往裡面扔，他說凡是合數通過篩子以後就會從網子裡面篩掉，留下的是素數，這個就是著名的埃拉特斯特尼篩法。
這個岐管篩子是把偶數往裡面扔，哥德巴赫猜想說，大於4的偶數一個也不會漏出篩子，除了6=3+3以外，其他偶數都是可以在不同的素數區域被攔截。例如8會在區域2也就是素數3和素數5（第三個區域）被攔截；偶數10會在素數3和素數7的兩個區域之間被攔截；。.。總之，無窮多個偶數都逃不脫這個網子，沒有一個偶數可以漏到外面去。
數論與圖論已經融合一起了。
5，與費馬大定理聯繫起來
這個還不算神奇，岐管的內部空間我們記為
，外部空間記為
，它有很多洞,可以有無窮多個洞，可以有無窮多個空間維度
，宇宙內外整體記為1，就是說
，這個叫做費馬曲線，它是由費馬大定理
同時除以
得到的。
費馬大定理與哥德巴赫猜想聯繫起來了。
費馬大定理的岐管就是m理論岐管
物理學家認為，宇宙是10維空間或者11維空間，或者26維空間等5個版本。還有物理學家認為有無窮多個維度的空間。他們管這個理論叫做玄理論或者M理論，是把廣義相對論與量子理論結合一起的終極理論，霍金說是最後的理論。
在弦/m理論的11維空間裡，有4維空間的伸展，7維空間捲縮起來的。 幾何體的拓撲性質同粒子緊密相關。例如，這種粒子幾何體有幾個洞，決定著粒子世代的數目，在這些捲縮維度的空間裡所採取的幾何構型決定著弦或者膜能夠有什麼樣的震動模式，從而決定著各種粒子的質量、自旋、以及電荷等各種相互作用的耦合常數。
原來，不僅僅自旋和同位旋等內部變數和內部空間都出自這些多維空間的幾何學，而且粒子的電荷質量等性質，無一不是從這裡產生出來的，不僅僅如此，人類生活本身也通過三維空間和一維時間都是從類似的幾何體的構造中生長出來的。 我們生活在高維宇宙的一小片中，大到銀河宇宙，小至原子夸克，都是 弦線構成的。
1、計算岐管中的線段需要黎曼猜想
數學家考慮的是怎樣計算這個岐管上的區域或者計算區域上面的一個點或者一條線。如果岐管上某一個區域n，在n上的一個點是
，因為這個岐管有無窮多個維度，或者很多維度，要定位這個點，就要考慮它的管壁——實部，還有考慮它的內外空間位置——虛部，即
，
，
表示虛數。
黎曼猜想！
在弦/m理論中，管壁就是膜，如果把膜上面的一個點定位，或者在管壁上畫出一條線，假設這個點是在區域的管壁上，膜是一個沒有厚度的管壁，管壁上的點就是實部，管壁內外就是虛部。
管壁上實部為1/2，因為宇宙等於1這個管壁就是實部α，在中間的位置，確定這個點的位置還有考慮管壁內外空間結構，就是虛部，要計算這個零點，就要用黎曼函式來運算，黎曼猜想！
黎曼猜想與費馬大定理聯繫起來了。這個方法的重要意義在於可以藉助幾何拓撲方法構造一個適合黎曼猜想的結構空間。
2、與歐拉公式聯繫起來
虛部怎麼計算呢？岐管內部看成一個圓管，虛部是什麼？它至少應該有管道內或者管道外中的一個參數。假設管道截面是一個圓，管道
內的截面圓依然是二維平面，在岐管上的一個點，就是一個圓。大家知道歐拉公式嗎？
以
開始，以相對速度
，走了時間（虛時間），再加1，回到原點（見右圖）。
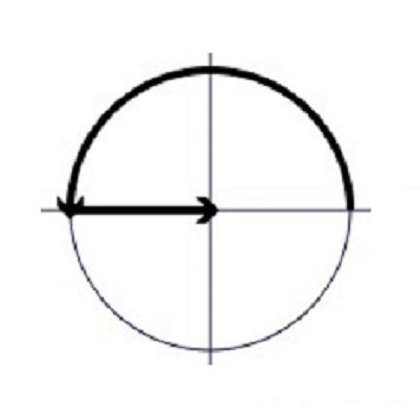
歐拉公式運行圖
虛時間是為了對應時間起點（大爆炸）而定義的一個概念。在虛時間這個概念體系里，在比三維更高的維度空間，時間並不是一條直線，而是一個閉合的圓，沒有起始也沒有終結，宇宙的起點如果源自大爆炸，那在此之前的時間將無法定義。因此，為了解決奇點之前時間應該如何，引用到了複數的概念。
如果走的路程超過了，比如4，
。於是：
。
（3）式看似荒唐，其實是虛時間理真實的時空穿越，現在的人
與過去的人
在同一時空相遇。也可以理解為兩個光量子糾纏，只要知道一個就可以知道另外一個。
人類生活在費馬大定理的宇宙空間，出門旅行（星際）需要用黎曼猜想計算路程，在歐拉公式協助下，穿過哥德巴赫猜想的蟲洞。（作者在德國參見霍奇猜想套用）
本文作者在德國，參見本版原創
黎曼猜想是二階邏輯問題
由於黎曼猜想屬於二階邏輯問題，所以無法證明
1，首先，因為，主項是一個集合概念的命題是無法證明的，因為集合概念的每一個個體不是必然具有這個概念的基本屬性。就決定了必須一個個去證明。
2，黎曼猜想的 “零點” 也是一個集合。零點是這個對象上的函式，按照通常數學中定義，一個n元函式就是從論域A的個體的所有n元組的集合至A的一個映射。當我們用“所有個體”“存在個體”，量詞加在論域的個體上，稱為一階量詞。“
” 所有函式”，“存在函式”，“所有關係”，“存在關係”是二階量詞，即二階邏輯。
黎曼所說的“所有零點”就是“所有函式”的二階量詞，黎曼猜想已經超出了G弗雷格建立的一階邏輯形式系統（即謂詞演算），涉及極為複雜的邏輯系統，一般的數學家對此毫無所知。（二階邏輯問題與貨郎擔問題，圓周率問題，詳見數學證明）
基本特點
將數學最重大問題與物理學最重大問題融合
