基本介紹
- 中文名:里斯變換
- 外文名:Riesz transform
- 適用範圍:數理科學
定義,希爾伯特變換,
定義
設 ,函式 f 的里斯變換定義為
,函式 f 的里斯變換定義為




里斯變換是希爾伯特變換在高維空間中的推廣。
希爾伯特變換
[Hilbert transform]
設 ,f 的希爾伯特變換定義為
,f 的希爾伯特變換定義為



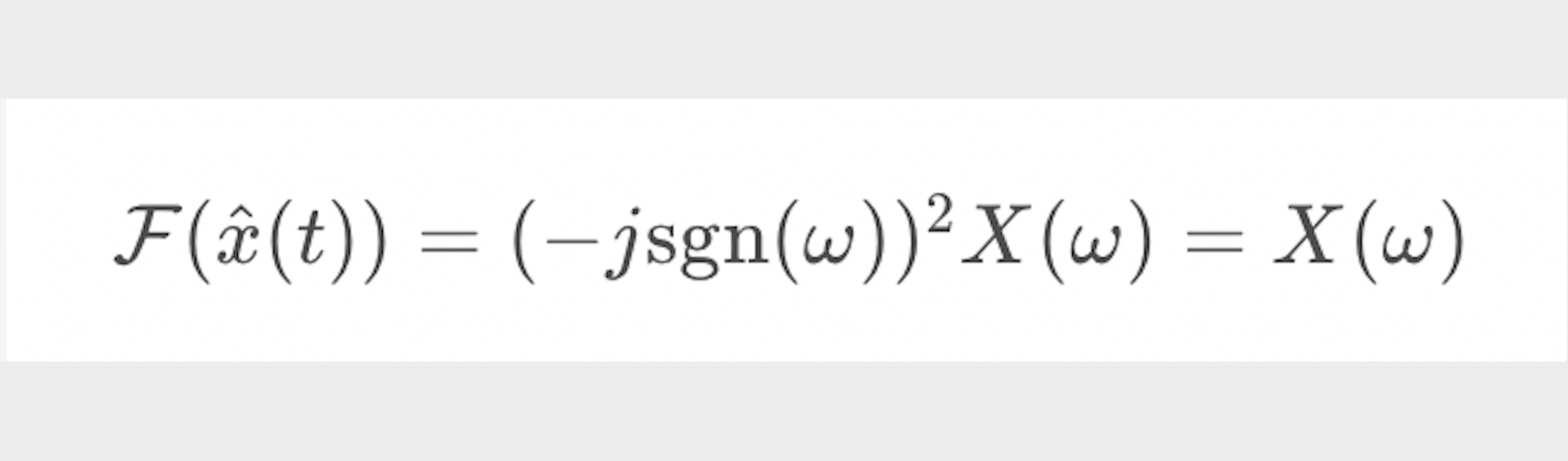
當 時,可證
時,可證


希爾伯特變換是調和分析領域中一種重要的積分變換,其在數學、物理及其工程領域中均有重要套用。








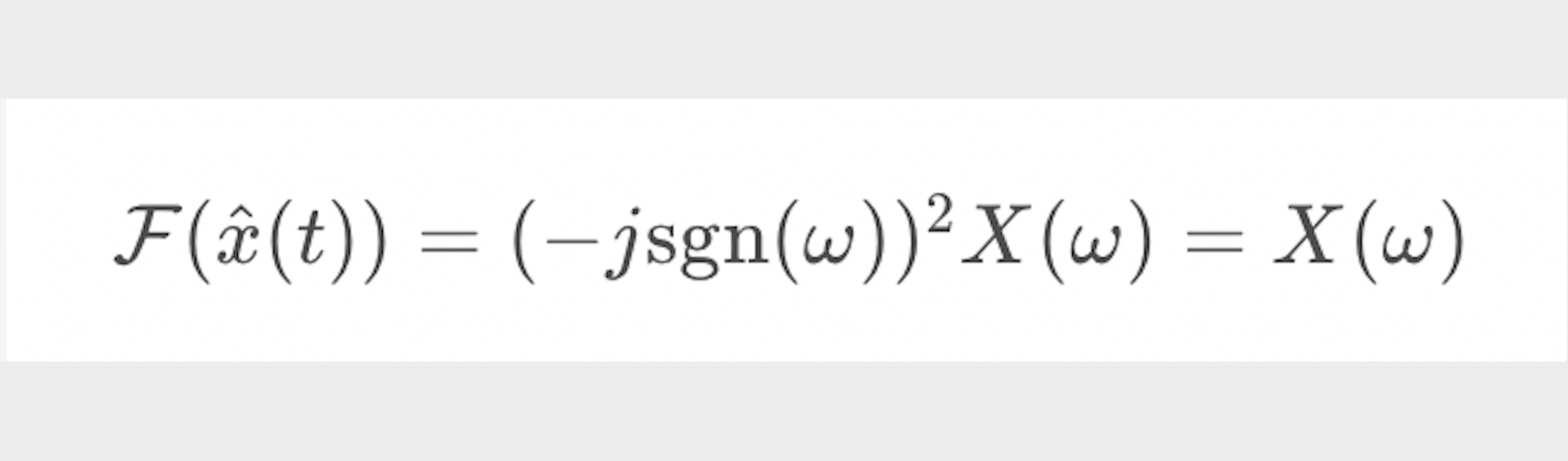


里斯變換是一種積分變換,屬於微積分學科。當n=1時,里斯變換恰恰就是熟知的希爾伯特變換,可見里斯變換的概念是希爾伯特變換的推廣。定義設 ,函式 f 的里斯變換定義為 其中 是伽馬函式, 。里斯變換是希爾伯特變換在高維空間...
傅立葉變換的限制定理(restriction theorem ofthe Fourier transform)傅立葉變換大小的一種描述,是研究多元函式傅立葉積分的博赫納一里斯平均L0收斂的重要工具.設S是R”的光滑子流形.d。是其上導出的勒貝格測度.如果對每一個施瓦茲...
是原始信號的希爾伯特變換。它在雷達信號處理、聲吶信號處理等領域較為常用。與解析信號類似,單演信號定義為高維信號 (n≥2)與其Riesz變換(里斯變換)的線性組合,若以二維信號(如圖像)為例,,則單演信號可表示為 其中 構成的是三...
他首先證明多元三角級數球形和的唯一性定理,並揭示了多元傅立葉級數的里斯- 博赫納球形平均的許多特性。傅立葉級數曾極大地推動了偏微分方程理論的發展。在數學物理以及工程中都具有重要的套用。公式 給定一個周期為T的函式x(t),那 ...
運算元內插,證明運算元有界性的一種數學方法。如果運算元T是Lp到Lq的有界運算元,即對所有的f∈Lp,有Tf∈Lq,且滿足 式中 M是 運算元的界,與 f無關,就稱 T是強( p, q)型的。最早也是最典型的 運算元 內插定理是里斯-索林定理。里...
