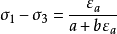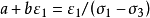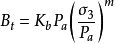提出過程
鄧肯-張模型是一個非線性本構模型,既然是一個本構模型,可想而之他反應的是
應力與應變之間的關係。說它是非線性的,那么反映應力應變關係的模量就不是一個常數E那么簡單。在介紹該模型之前,先要介紹一個概念,就是反映非線性關係的增量廣義胡克定律:
1963年,康納(Kondner)根據大量土的三軸試驗的應力應變關係曲線,提出可以用雙曲線擬合出一般土的三軸試驗(σ1-σ3)~ε即:
其中,a、b為試驗常數。對於常規三軸壓縮試驗,εa=ε1。鄧肯等人根據這一雙曲線應力應變關係提出了一種目前被廣泛的增量彈性模型,一般被稱為鄧肯-張(Duncan-Chang)模型。
研究現狀
目前描述土的應力-應變關係的數學模型有許多種,歸納起來有兩大類:一類是彈性模型,它包括線性彈性模型和非線性彈性模型,其中較典型是E-μ模型和K-G模型;另一類是彈塑性模型,其中較典型的有Cambridge模型、清華模型、沈珠江的雙屈服面模型等。從實際套用來看,彈塑性模型能較好地反映土的實際變形特徵和內部機理,以及土體的硬化、軟化和剪脹性質,具有廣闊的發展前景,但參數求取相對較困難,計算過程複雜;彈性模型中非線性彈性模型既能比較好地模擬土的實際力學性質,又具有形式簡潔參數少的特點,在工程計算分析中被廣泛採用,因此有很多學者對非線性彈性模型進行了研究。
土體的K-G模型就是在非線性彈性分析時把應力分解成球張量p和偏張量q兩部分,應變也分解成球應變(體應變)εv和偏應變(剪應變)εs,相應地採用體積變形模量K和剪下模量G代替工程上常用的變形模量E及泊松比μ。國內對K-G模型的研究取得了一些有價值的成果。
Duncan—Chang在Kndner應力、應變雙曲線假定基礎上提出雙曲線E-μ模型。Duncan等人通過模型試驗並使用Duncan—Chang模型進行計算,發現荷載較高時,計算的沉降值偏大。由於測定土的變形模量E和泊松比μ受試驗方法等因素的影響較大,而實際套用中恰當的模量和泊松比的選定又比較困難,因此有人認為土的應力-應變特性利用楊氏模量及泊松比是不恰當的。在排水條件下,若發生強烈的剪脹現象時,土的μ值可等於或大於0.5,這時用E-μ模型就遇到很大的困難,在有限元計算中某些單元應力狀態達到破壞時,會得到不合理的結果。在三軸試驗中,模型能描述不同應力路徑關係,但體變預測不準,泊松比值誤差較大。Duncan等人對模型進行了修正,即採用剪下體積模量的K-G模型,因鄧肯一張非線性彈性E-μ和E-B模型(下面簡稱E-μ和E-B模型)都不能反映土的剪脹和應變軟化。雖然E-μ和E-B模型存在許多局限性,但其模型參數較簡單,概念清楚,各個試驗參數都有一定的物理意義與幾何意義,可以通過常規三軸剪下試驗獲得而套用最為廣泛,除套用於岩土體的應力、應變研究外,也套用於瀝青混凝土等材料的應力、應變性質的研究。
鄧肯—張模型中E—B的模型簡介
1、雙曲線應力應變關係
在三軸試驗中,在不同的周圍壓力σ3下,一般可測得一組應力—應變關係曲線。固結排水試驗得到土的應力—應變關係曲線通常接近雙曲線,因此假定土的應力—應變關係滿足如下的雙曲線方程:
式中:
(σ1-σ3)——主應力差;
ε1——相應於σ1-σ3的軸向應變,由試驗測定;
a、b——決定於土性質的試驗參數。
把上式改寫成:
ε1和ε1/(σ1-σ3)關係呈直線方程,將實測的ε1和ε1/(σ1-σ3)繪製在同一坐標下,則所得直線在ε1/(σ1-σ3)坐標軸上的截距就是a,所得直線的斜率為b。
按照初始切線模量Ei的定義,當ε1→0時,由上式得:
Ei=d(σ1-σ3)/dε1|ε1→0=1/a(3)
而當ε1→∞時,(σ1-σ3)u=ε1/(a+b·ε1)|ε1→∞=1/b
至此,康得納(Kandner)和柴拉斯高(Zelasko)1963年指出的雙曲線應力—應變關係可表達為:
σ1-σ3=ε1/(1/Ei+ε1/(σ1-σ3)u)
2、初始模量Ei
簡布(Janbu)通過試驗研究在1963年指出,土的初始模量都是側限壓力的指數函式,並可用下式表示:
Ei=K·Pa(ε3/Pa)n
式中:
Pa——大氣壓力;
K、n——無因次基數和無因次指數,是決定於土質的試驗常數。由lg(Ei/Pa)與lg(σ3/Pa)直線關係確定,其截距為K,斜率為n。
3、切線模量Et
土的非線性特性就是指變形模量E隨應變ε1(或σ1-σ3)而變化,常用切線模量Et表示。
土樣破壞時的應力稱為破壞應力差(σ1-σ3)f,它總是比應力差極限(σ1-σ3)u小,令:
Rf稱為破壞比,其值一般在0.75~1.0之間。根
據摩爾—庫侖準則,抗剪強度可表示為:
(σ1-σ3)f=2ccosφ+2σ3sinφ/(1-sinφ)
式中:c、φ———土體的粘聚力和內摩擦角。
將上述公式後整理,即得由鄧肯(Duncan)和張(Chang)於1970年提出的土體非線性模型:
4、切線體積模量Bt
在土體的應力、變形有限元分析中,需要一個反映土體積變化的參數。起初,鄧肯—張模型中採用切線泊松比μt,後來發現不太理想,繼而採用切線體積模量Bt作為計算參數。在三軸試驗中,體積模量表示為
式中:Kb———決定於土質的試驗常數,分別由lg(Bt/Pa和lg(σ3/Pa)直線的截距和斜率確定。計算Bt時,通常取σ1-σ3=0.7(σ1-σ3)f時的體應變。
局限性
(1)鄧肯-張模型是在軸向應力增加,而側向應力不變的情況下獲得的,但在現實中,土體往往經歷的應力路徑不是軸向壓縮,還有可能是其它的應力路徑(側向卸載、側向載入、軸向卸載、軸向載入),這就造成該模型不能很好的模擬它們。
(2)由於該模型是建立在增量廣義胡克定律基礎上的變模量的彈性模型,無法反映土的剪脹性。
套用
套用鄧肯一張非線性模型近似計算路基沉降:
土體在路堤荷載作用下的變形過程,伴隨著主應力大小的不斷變化及主應力方向的不斷偏轉,土的彈性模量及泊松比也隨之改變。為模擬這一過程,得出位移在路基橫向的近似分布情況。假定如下:
①路堤填築荷載引起的附加應力場可近似採用同樣荷載作用下線上彈性半空間無限體所產生的附加應力場。
②土體力狀態應力—應變本構關係符合鄧肯一張非線性模型。
③路基橫向斷面受力狀態為平面應變狀態。
壓縮試驗所得的e-p曲線在一定程度上體現了土體的非線性特性,可考慮用它來確定非線性變形參數K、n。在壓縮試驗中.土體處於無側向變形狀態,靜止側壓力係數近似表示為:
k0=1-sinφ(對砂土)
k0=0.95-sinφ(對粘土)
相應的泊松比為:
μ0=K0/(1+K0)
費正華,鄧水明等人把此式作為初始泊松比,切線泊松比為:
μr=μ0+(0.49-μ0)S0
沉降量的計算步驟如下:
①計算各土層的有關計算參數。
②對土層進行離散;計算各土層原始地應力;對地下水位以下的土層採用浮容重;對路基橫向計算點循環;計算附加應力。
③對各層單元循環,判斷所屬土層,選用相應的計算參數。
④對附加應力進行離散,分解成若干應力增量,對應力增量進行循環;計算各層單元每次增量對應的初始應力及對應的應力水平和切線彈性模量、切線泊松比;然後,由土體增量形式的本構方程反算出在該應力增量作用下產生的豎向應變和豎向變形。對豎向變形之和加以計算,即可得各橫向計算點下的總位移量。
其地基沉降量計算實際上採用的是E-μ模型,雖然E-μ模型存在自身缺陷,但其計算結果與實驗所得結果較為吻合。鄧肯-張模型套用到此工程中,主要解決了過去根據工程經驗取係數值的盲目性,較規範算法更為精確。