部圖

部圖(partite graph)是一類特殊的圖，即一個圖的節點集可分成若干個子集，使得每一條邊的兩端點不在同一子集內，若一個圖的節點集能分成k個兩兩不交的非空子集，使得這個圖的每一條邊的兩端點不在同一個子集內，則稱這個圖為k部圖。若k=2，則稱這種k部圖為二部圖；若k=3，則稱這種k部圖為三部圖，若在一個k部圖中，任一節點與其他部的所有節點都相鄰，則稱它為完全k部圖。

基本介紹

• 中文名：部圖
• 外文名：partite graph
• 所屬學科：數學
• 所屬問題：組合學(圖與超圖)
• 簡介：一類特殊的圖

基本介紹

若圖G的點集V有一個劃分

所有V_i非空，且<V_i>均為全不連通的，則稱G是一個n部圖，2部圖又稱雙圖，(1)稱為G的一個n部劃分，G也記作G=()。顯然任何p階圖是一個p部圖。若n₁<n₂≤p，易知任一n₁部圖也是n₂部圖。

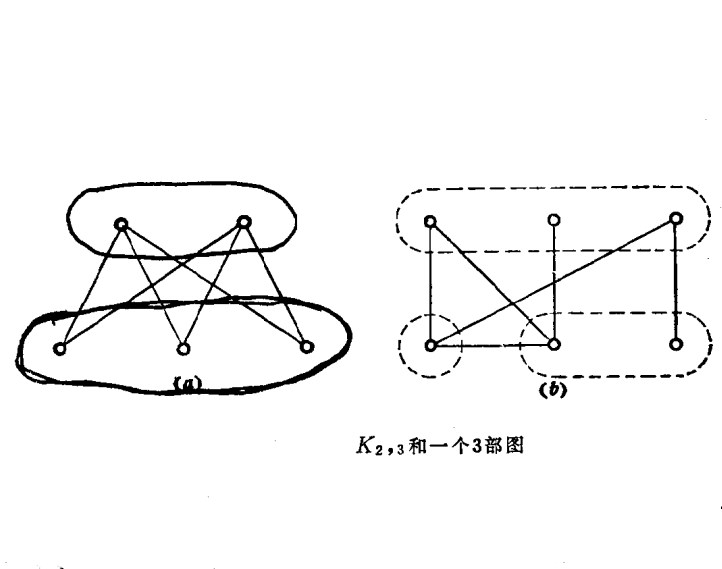
如果在一個n部圖G=()中，，任何兩點u∈V_i，v∈V_j，i≠j，i=1，2，…，n，均有u adj v，則稱G為完全n部圖，記作。圖1中給出了完全2部圖K_2,3(a)和一個3部圖(b)。

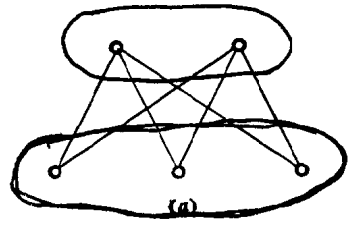圖1（a）

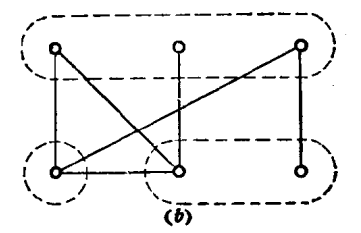圖1（b）

相關定理

一般來說，一個n部圖的n部劃分不是唯一的，但對連通雙圖有下列定理。

定理1 連通雙圖G=(V₁，V₂；X)的2部劃分唯一，

證 取v∈V₁，由於G是連通的，對任何u∈V₁∪V₂，有聯結v和u的道路，故d(v，u)有定義，因為任何一條以v為起點的道路交替地經過V₁和V₂的點，可知一點u∈V₂若且唯若d(v，u)是奇數。這個準則唯一地決定了G的2部劃分。證畢。

雙圖的特徵由下列定理給出．

定理2 一個圖G是一個雙圖若且唯若它不含有長度為奇數的圈。

定理3任何不含有三角形的(p, q)圖G有

當G=K_m,m或K_m,m+1時等號成立。

定理3可以推廣，事實. 上，它可以由下面的定理6推出。但定理6的證明較定理3複雜得多。設G和H是兩個p階圖， 若存在V(G)到V(H)的一個一一對應μ，使對任何點u∈V(G)，有

deg_Gu≥deg_Hμ(u)，

則稱G的度序列優於H。

現在我們對n≥0遞推地定義不含K_n+1的圖H的厄爾多斯

(Erdös)圖E(H)，n=0時，若H不含K₁，則H是全不連通的，令E(H)=H， n>0吋，若H不含K_n+1，在H中取一點v，使deg v=Δ(H)，由v的郤域N(v)導出的子圖<N(v)>中不含K_n，故E(<N(v)>)已經定義，再加上p(H)-Δ(H)個點，使它們毎一個均與E(<N(v)>)的毎個點鄰接，即得到一個E(H)。一般地，E(H)不必唯一，顯然p(E(H)= p(H)，今有下列引理。

引理4 對任何不含K_n+1的圖H，E(H)是一個完全n部圖，且E(H)的度序列優於H，此外，若更有E(H)的度序列與H的度序列相同，則

引理5 p階n部圖G有最多的線若且唯若G≌T_n,p。

定理6(托蘭(Turán)定理)若p階圖G中不含K_n+1，則|X(G)|≤|X(T_n,p)|，等號若且唯若G≌T_n,p時成立。

定理7對任何雙圖G=(V₁，V₂；X)，存在一個正則雙圖H，使G⊂H，且deg H=Δ(G)。