那羅延數

那羅延數是組合數學問題中常用的一組計數序列。

基本介紹

• 中文名：那羅延數
• 外文名：Narayana number

提出命名

在組合數學中，那羅延數以及由那羅延數形成的那羅延三角，經常會出現在各種各樣的計數問題中。那羅延數和那羅延三角是以印度數學家 T.V. Narayana(1930–1987)的名字來命名的。

計算公式

那羅延數N(n,k)的計算公式為

主要性質

那羅延三角中每一行的和為卡特蘭數，即

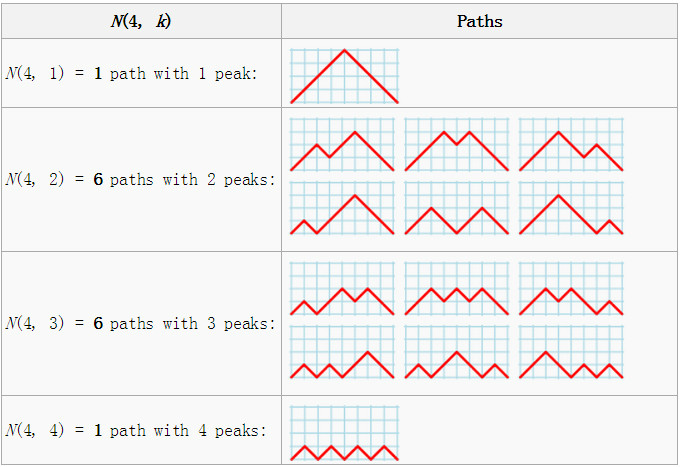
由下面的例子可以證明上面的公式。考慮從(0,0)到(2n,0),只有(1,1)和(-1，-1)兩種移動方式，且要求運動軌跡不能低於x軸，一共有多少種情況。

當n=4時，一共有1+6+6+1=14種，如下圖，恰好等於。

事實上，這個問題等價於求從(0,0)到(n,n)的位於對角線上方的非降路徑數，即。

主要舉例

那羅延三角

那羅延三角(OEIS A001263)的前8行為

k = 1 2 3 4 5 6 7 8

n = 1 1

2 1 1

3 1 3 1

4 1 6 6 1

5 1 10 20 10 1

6 1 15 50 50 15 1

7 1 21 105 175 105 21 1

8 1 28 196 490 490 196 28 1

()字元串

在由n對"(“、”)"組成的字元串中，共有k對“(“與”)”相鄰，這樣的字元串一共有N(n,k)個。例如n=4,k=2時，N(n,k)=6,分別為

()((())) (())(()) (()(())) ((()())) ((())()) ((()))()