在決策理論中,在不確定性下作出決定 - 如果有關最佳行動方案的信息在採取固定決定之後到達 - 人們經常會遇到情緒反應的遺憾。 遺憾準則理論提出,當面對一個決定時,個人可能會期待遺憾,從而選擇他們消除或減少這種可能性的願望。 遺憾是一種負面的情緒,具有強大的社會和聲譽組成部分,是人類從經驗和人類心理學角度學習風險規避的核心。 意識到後悔的預期創造了一個反饋循環,將情感領域(通常被模仿為僅僅是人類行為)的遺憾提升到決策理論中被模仿的理性選擇行為的領域。
基本介紹
- 中文名:遺憾準則
- 外文名:Regret criterion
- 目的:儘量減少決策者的遺憾
- 準則內容:min-ma
- 領域:決策理論
- 套用:凸最佳化
簡介,歷史,證據,預期的遺憾與經驗的遺憾,實例,
簡介
在決策過程中,當某一種狀態可能出現時,決策者必然要選擇心中想要的方案。但如果決策者由於決策失誤而沒有選擇心中想要的方案,則會感到遺憾和後悔。遺憾準則的基本思想就是在於儘量避免決策者的遺憾,使決策者絕不後悔。
歷史
對不確定性的理論模型選擇感到遺憾,考慮到預期後果的影響。 它最初由Graham Loomes和Robert Sugden David E. Bell和Peter C. Fishburn同時開發,隨後又被其他幾位作者改進。
一般來說,這些模型將效用函式的遺憾術語納入到不確定性解決方案中,對效用函式產生負面影響,並對最佳替代結果產生積極影響。 這個遺憾術語通常是減去傳統效用指數的增加,連續和非負的函式。 這些類型的偏好總是違反傳統意義上的傳統,儘管大部分都是較弱的版本。
證據
對激勵和假設選擇的若干實驗證明了這種效應的大小。
第一次價格拍賣的實驗表明,通過操縱參與者期望獲得的反饋,觀察到平均出價的顯著差異。特別是,“失敗者的後悔”可以通過向拍賣所有參與者揭示中標,從而向失敗者揭示他們是否能夠獲得利潤,並且可以獲得多少(一個參與者有估價為50美元,出價30美元,發現中標價格為35美元,也將了解到,通過投標超過35美元,她可以賺取高達15美元)。這反過來又允許遺憾的可能性,如果投標人正確預測,如果沒有提供有關中標的反饋來降低遺憾的可能性,那么他們往往會提高出價。
在彩票決策中,實驗也提供了預期遺憾的證據。如在第一次價格拍賣的情況下,對解決不確定性的反饋差異可能導致遺憾的可能性,如果這是預期的話,它可能會引起不同的偏好。例如,當面對40美元的確定性和硬幣拋擲之間的選擇,如果結果被正確猜測並且$ 0否則支付100美元,那么特定的支付方式不僅可以最大限度地降低風險,而且可以遺憾,因為通常是硬幣不會被拋棄(因此不確定性不能解決),而如果選擇了硬幣投擲,則支付0美元的結果將會引起遺憾。如果硬幣被拋棄而不考慮所選擇的替代方案,那么替代收益將永遠是已知的,那么沒有選擇會消除遺憾的可能性。
預期的遺憾與經驗的遺憾
對於人們認為自己負責的選擇和行動,預期的遺憾往往被高估了。人們特別有可能高估他們在缺少期望結果的時候會感到遺憾。在一項研究中,通勤人員預測,如果他們錯過了1分鐘以上的火車1分鐘以上的距離,而不是5分鐘左右的火車,那么他們會感到更遺憾,但實際上錯過了1或5分鐘火車的乘客經歷了(等於)遺憾通勤員似乎高估了他們在缺少火車的時候會覺得很遺憾,因為他們傾向於低估他們將火車列入外部原因的程度(例如,丟失錢包或花更少的時間在淋浴中) 。
實例
以下是對遺傳概念如何用於設計線性估計器的說明。在這個例子中,問題是從已知噪聲協方差結構的噪聲線性測量中構造有限維參數向量x的線性估計器。使用均方誤差(MSE)測量x的重建損失。已知未知參數矢量位於以零為中心的橢圓E中。遺憾被定義為不知道參數x的線性估計器的MSE與知道x的線性估計器的MSE之間的差異。此外,由於估計器被限制為線性,所以在後一種情況下不能實現零MSE。在這種情況下,凸最佳化問題的解決方案給出了最優的最小值遺憾線性估計器,可以通過以下參數來看待。
根據假設,觀察到的矢量y和未知的確定性參數矢量x的線性模型為:

其中H是具有全列秩m的已知m×n矩陣,並且w是具有已知的零均值隨機向量協方差矩陣 。
。

讓: 是y關於x的線性估計,其中G是某些m×n矩陣。該估計器的MSE由下式給出:
是y關於x的線性估計,其中G是某些m×n矩陣。該估計器的MSE由下式給出:


由於MSE明確地依賴於 x,因此不能直接將其最小化。相反,可以使用遺憾的概念來定義具有良好MSE性能的線性估計器。為了在這裡定義遺憾,考慮知道參數x的值的線性估計器,即矩陣 G可以明確依賴於x:

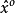



將這個G(x)替換成MSE ^ {o},得到:

這是可以通過線性估計知道x的最小MSE。在實踐中,這個MSE是無法實現的,但它作為最優MSE的約束。使用G指定的線性估計值的遺憾等於:

