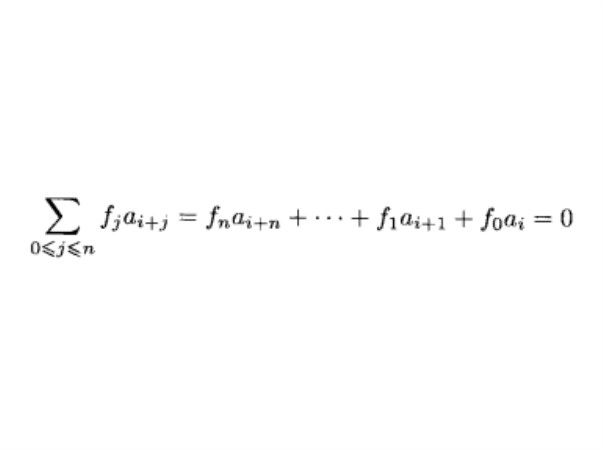遞推列

遞推列(recursive sequence)亦稱遞歸列，指由前面的項能推出後面的項的數列，線性遞推列是特殊的遞推列。例如等差數列與等比數列就是遞推列，也是線性遞推列。

基本介紹

• 中文名：遞推列
• 外文名：recursive sequence
• 所屬學科：數學（線性代數）
• 別名：遞歸列
• 簡介：由前面的項能推出後面的項的數列

基本介紹

遞推列指由前面的項能推出後面的項的數列，對所有n>p，滿足形如a_n=f(a_n-1，a_n-2，…，a_n-p)的關係式的序列{a_n}，其中f為某個函式。p是某個固定的正整數，a₁，a₂，…，a_p為已知數，p稱為這個遞推列的階數，上述關係式稱為遞推公式，給定a₁，a₂，…，a_p，可以從它得到所有a_n。

形如a_n+c₁a_n-1+c₂a_n-2+…+c_pa_n-p=0(c₁，c₂，…，c_p是常數)的遞推公式稱為線性遞推公式，相應的序列稱為線性遞推列，最簡單的遞推列是一階遞推列，即滿足a_n=f(a_n-1)的序列{a_n}，它又稱疊代列。等差數列與等比數列都是線性的疊代列。

根據以上定義，將F和V均取為Q，則我們熟悉的Fibonacci序列是線性遞推列，構成它的一個特徵多項式。我們知道，對於一個線性遞推列，在已知其特徵多項式及最初的幾個取值時，可以通過遞推的方法快速計算其後繼序列，下面我們舉一些線性代數中涉及的線性遞推列的例子，它們在後而的算法中扮演了重要角色。

相關介紹

【例1】本例給出線性代數中一些熏要的線性遞推列，這裡最關鍵的是利用了線性代數中的Caley-Hamilton定理[，以下F均表示一般域。

1．取V=F，A∈V為任意方陣，則為線性遞推列，A的極小多項式與特徵多項式都是a的特徵多項式。

2．設V=F，A∈F，b∈F為任意向量，注意到(A)的任意特徵多項式也將(Ab)化為零，故(Ab)也為線性遞推列。由a的元素生成的V中的線性子空間稱為A與b的Krylov子空間。

3．設V=F，A∈F，b，u∈F為V中的任意向量，則(Ab)的任意特徵多項式同樣將(uAb)化為零，故(uA)b也為線性遞推列。