遞推估計算法

給(t),F(t),(t)和w(t)不同的值就得到各種不同的方法：①遞推最小二乘法；②遞推增廣最小二乘法；③遞推近似極大似然法；④遞推輔助變數法；⑤遞推廣義最小二乘法；⑥卡爾曼濾波參數估計；⑦隨機逼近法；⑧模型參考適應法；⑨時變參數遞推估計法。

基本介紹

• 中文名：遞推估計算法
• 外文名：Recursive Estimation Algorithm
• 性質：數學術語
• 套用：工程與通信問題

概述

遞推估計算法recursive estimation algorithm

利用時刻t上的參數估計、存儲向量與時刻 t+1上測量的輸入和輸出值u(t+1)和y(t+1)計算新參數值(t+1),再根據(t+1)計算出新參數值(t+2)，直到獲得滿意的參數值為止。這種算法的每一步計算量都比較小，能夠使用小型計算機進行離線或線上參數估計，可以估計時變參數，也可以實時估計適應控制器的參數（見適應控制系統）。20世紀60年代，遞推估計算法得到迅速發展，到了70年代產生了許多不同的方法，例如，有離線方法的各種變形、卡爾曼濾波法、隨機逼近方法和模型參考適應參數遞推估計法等。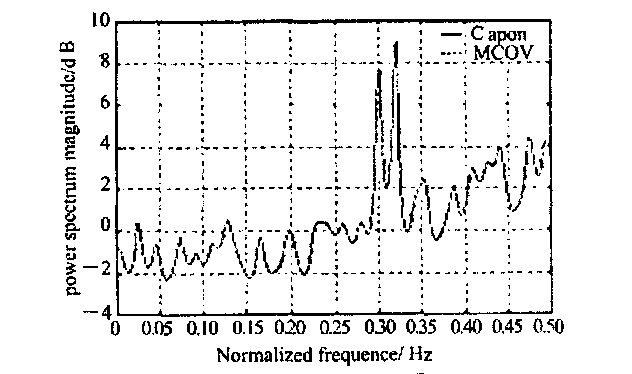

遞推估計算法

遞推估計算法的各種方法可以用一個統一的公式來描述：

套用領域

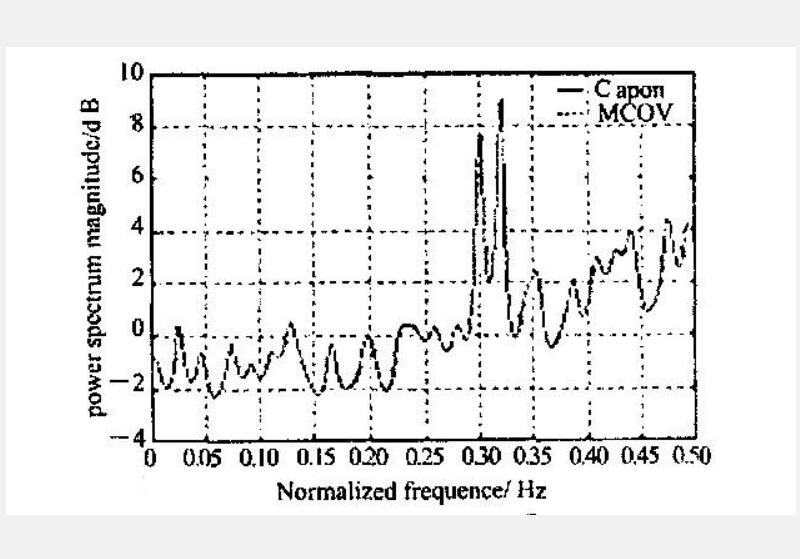
在許多工程與通信問題中都需要求解由信號構成的矩陣的特徵向量，如何快速準確地計算特徵向量在工程實際問題的解決中有著重要意義。當今求解特徵向量的方法普遍存在計算量很大的問題,它們大都是對由特徵向量張成的子空間做出估計,或者是通過複雜的運算對特徵向量做出直接估計，很難將其套用於實時信號處理中。具有較小計算複雜度並對特徵向量做出直接遞推估計的方法並不多見。

提出兩種新的特徵向量遞推估計算法:一種基於KLT 與滑動DCT的相似關係,將特徵向量等效為自適應濾波器的權向量,通過合理選擇該濾波器期望回響遞推求解出特徵向量;另一種通過對子空間疊代法進行合理改進,並將壓縮技術套用到子空間疊代法中,遞推求解出特徵向量。同當前的特徵向量求解方法相比(如奇異值分解法),兩種算法都有效地減少了運算量和計算複雜度,容易實時實現,且具有很高的估計精度。將兩種算法套用到MUSIC 譜估計中,通過計算機仿真實驗可知,提出的算法進行譜估計精度要高於標準的MUSIC 譜估計精度,且計算量大大減小,由此驗證了算法的有效性和優越性。