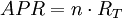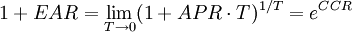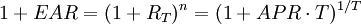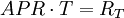連續複利收益率

R′=ln(1+R)(1)

此處，ln代表自然對數函式，證明如下：

以C0 元投資一期，並複利計息一次的期末資金為：

C1 = C0(1 + R) (2)

以連續複利生息一期所得的期終資金應為

C1 = C0eR' (3)

(2)式等於(3)式，可得(1)式。所以，若單期收益率為R，則其對等的連續複利收益率應為(1+R)的自然對數，即ln(1+R)。

連續複利收益率在投資研究的領域中運用十分廣泛。其原因之一在於，它的機率分布較接近於常態分配，對金融經濟學的理論發展與實際驗證的簡化具有相當大的幫助。

基本介紹

• 中文名：連續複利收益率
• 外文名：Continuously compounded rate of return，CCR

複利收益率

連續複利收益率（Continuously compounded rate of return，CCR）

年度百分率

年度百分率(annual percentage rate,APR)

有效年利率

有效年利率（Effective Annual Rates，EAR）

T為持有期

短期投資利率常用APR來表示，一年有n=1/T期，每期利率為RT ,則

連續複利收益率

連續複利收益率

連續複利收益率

連續複利收益率

CCR = ln(1 + EAR)

參考文獻

1 孫伍琴,王朝暉,熊樂星.證券投資學.上海市：立信會計出版社,2008.