透鏡空間是數學中考慮的拓撲空間的一個例子。 該術語通常是指特定類型的三維多面體,但也可以定義為更高的維度。
在三維多面體的情況下,透鏡空間可以通過將兩個實心圓弧通過其邊界的同態粘合在一起而被可視化。 通常,如上所述,三球(3-sphere)以及S2×S1,因為它們是三維的,所以兩者都可以被計算。
基本介紹
- 中文名:透鏡空間
- 外文名:Lens space
- 領域:數學
- 實質:拓撲空間的一個例子
- 適用對象:通常是特定類型的三維多面體
- 相關名詞:拓撲空間
定義,定義,替代定義,空間分類,
定義
透鏡空間是數學中考慮的拓撲空間的一個例子。 該術語通常是指特定類型的三維多面體,但通常也可以定義為更高的維度。
在三維多面體的情況下,透鏡空間可以通過將兩個實心圓弧通過其邊界的同態粘合在一起而被可視化。 通常,如上所述,三球(3-sphere)以及S×S因為它們是三維的,所以兩者都可以被計算。
三維透鏡空間L(p,q)由Tietze在1908年引入。它們是第三種已知的三維多面體實例,它們不是由它們的同源組和基本組決定的 ,以及其同構型不是由其同構型確定的封閉多面體。J.W. 亞歷山大在1919年表明,即使他們具有同構的基本原理,儘管他們沒有相同的同構型,透鏡空間L(5; 1)和L(5; 2) 也屬於群體和同源。 其他透鏡空間具有相同的同構型(因而是同構的基本組和同源性),但不是同胚型,因此,它們可以被看作是與代數拓撲不同多面體的幾何拓撲的誕生。
根據基礎組和Reidemeister扭轉,有三維透鏡空間的完整分類。
定義
三維透鏡空間L(p; q)是Z/p在S3的商。 更準確地說,讓p和q成為互質整數,並把S3視為C2里的球。 然後在S3中Z/p由下式生成:
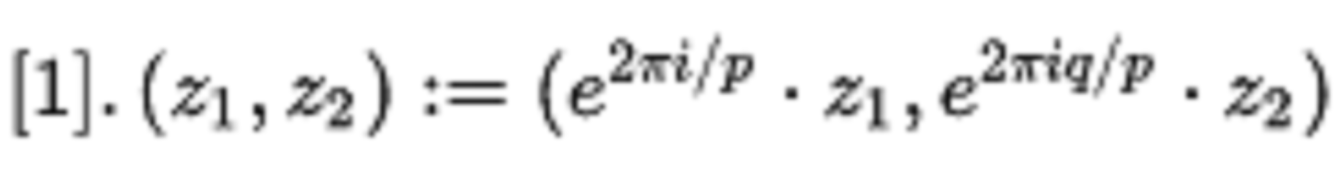
所得到的商空間稱為透鏡空間L(p; q)。
這可推廣到更高的維度,如下式所示:令p,q1,......qn是整數, 顯示方式qi是p的互補碼,並將S2n-1視為C n。 透鏡空間L(p, q1,......qn)是S2n-1中Z/p由下式生成:
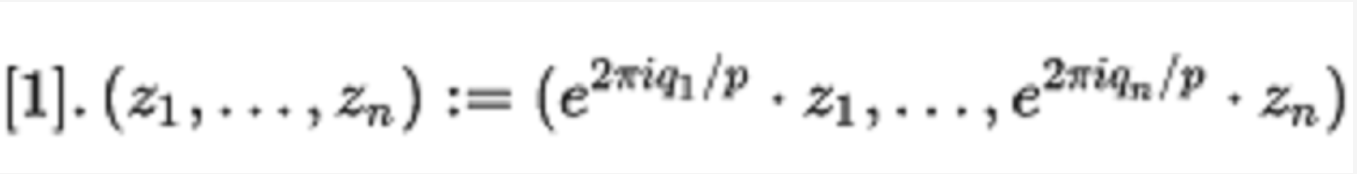
在三維中,我們有L(p; q)= L(p; 1,q)。
替代定義
三維透鏡空間L(p,q)通常被定義為具有以下識別的實心球:首先在實心球的赤道上標記p等距點,將它們表示為a0到ap-1,然後在 球,將連線點的測地線連線到北極和南極。 現在通過識別南極的北極和具有ai + q和ai + 1的ai + q + 1的點ai來識別球形三角形。 所得空間與透鏡空間L(p,q)是同態的。
另一個相關定義是將固體球視為以下實心雙錐體:構造平面規則的雙面多邊形。 直接在多邊形的中心上方放置兩點n和s。 通過將常規p邊多邊形的每個點連線到n和s來構造雙錐體。 填充雙錐體使其固體,並在邊界上給出與上述相同的標識。
空間分類
分類到同胚和同構等價是已知的,如下。 三維空間{\ displaystyle L(p; q1)和L(p; q2)是:
同構當量若且唯若


在這種情況下,他們是“明顯的”同構,因為人們很容易產生同構。 很難顯示這些是唯一的同型透鏡空間。
給出三維透鏡空間的同構分類的不變數是扭轉聯接形式。
同構分類更微妙,由Reidemeister扭轉給出。這是在(Reidemeister 1935年)中給出的,作為PL同構的分類,但在(Brody 1960)中被證明是一個同構分類。在現代,透鏡空間由簡單的同構型確定,並沒有正常的不變數(如特徵等級)或手術阻塞。
(Przytycki&Yasuhara 2003)給出了一個結理論分類:令C為透鏡空間中的閉合曲線,該透鏡空間提升到透鏡空間的通用蓋中。如果提升的結有一個簡單的亞歷山大多項式,計算對上的扭轉連結形式(C,C) - 那么這給出同胚分類。
另一個不變數是配置空間的同構型(Salvatore&Longoni,2004),表明同構同位素但不是同形晶狀體空間可能具有不同同構型類型的配置空間,可以由不同的Massey產品來檢測。
