一個數的逆對數(antilogarithm),是指一個正數的對數即等於已知數。也就是說,在b=logaN對數運算中(以a為底的對數),逆對數是已知對數b去尋求相應的真數N。
基本介紹
簡介,方法,相關知識,
簡介
一個數的逆對數,是指一個正數的對數即等於已知數。也就是說,在b=logaN中,逆對數是已知對數b去尋求相應的真數N。
即為對數運算的逆運算。一般可以通過逆對數表查得。
方法
由b的尾數查逆對數表確定N的前幾個有效數字;而由b的首數來確定N的位數:即當b的首數不小於0時,N的位數等於b的首數加一;當b的首數小於0時,N的第一個有效數字左邊0的個數等於b的首數的絕對值(包括小數點前的一個0)。
相關知識
對數通過簡化難度計算,有助於科學的進步,特別是天文學。 他們對測量,天體導航和其他領域的進步至關重要。
計算器和計算機之間的對數實際使用的關鍵工具是對數表。第一張這樣的表格由亨利·布里格斯在1617年由納皮爾發明之後編制而成。 隨後,表的範圍不斷擴大。 這些表格對於某個基數b(通常為b = 10),在某一範圍內以某種精度列出了數字x的logb(x)和bx的值。
例如,Briggs的第一個表包含1-1000範圍內所有整數的常用對數,精度為14位數。
由於函式f(x)= bx是logb(x)的反函式,所以稱為逆對數。
常數計算兩個正數c和d的乘積和它們的對數的和差。 乘積c*d或商c / d可以查找逆對數表:
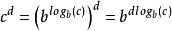
和
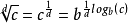
許多對數表通過分別提供x的特徵和尾數,即log10(x)的整數部分和小數部分來給出對數。log10(x)是x的特徵之一,它們的含義相同。 這擴展了對數表的範圍:給出了對於1到1000之間的所有整數x列出log10(x)的表,3542的對數近似為
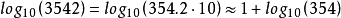
通過插值可以獲得更高的精度。
