迭核(iterated kernel)是由已知核經過逐次積分而得到的各種核。核是位勢論的基本概念。在位勢論中,所謂核,常指一般位勢的核。這時若K(x,y)≥0恆成立,則稱K為正核;令K′(x,y)=K(y,x)(K′稱為K的轉置核),若K′=K,則稱K為對稱核;當Ω為阿貝爾群且有K(x,y)=K(x-y)時,則稱K為平移不變核。
基本介紹
- 中文名:迭核
- 外文名:iterated kernel
- 領域:數學
- 學科:位勢論
- 方法:由已知核經過逐次積分而得
- 推廣:n次迭核、沃爾泰拉型n次迭核
概念,位勢論,核,歸納法,
概念
迭核(iterated kernel)是由已知核經過逐次積分而得到的各種核。設k(x,y)是線性積分運算元的核,令k1(x,y)=k(x,y),用歸納法定義:
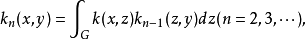
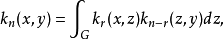
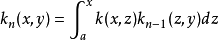
位勢論
現代分析數學領域的一個分支,主要研究各種形式的位勢(函式)和與其密切關聯的調和函式、上(下、超、次)調和函式族的各種性質及其套用。經典位勢論的主要研究工具是微積分,並與微分方程、複變函數論緊密關聯;現代位勢論以拓撲、泛函分析與測度論、廣義函式等為主要工具,與分析數學領域的諸多分支相互滲透並和隨機過程建立了深刻的內在聯繫。位勢論起源於物理學的萬有引力學說和靜電學,遠在1733年,拉格朗日(Lagrange,J.-L.)就注意到引力場是一個函式(稱為牛頓位勢)的梯度。在三維歐氏空間,一個單位質點εy的引力場在點x(x≠y)的牛頓位勢等於把一個單位質點從無窮遠移到點x所做的功,其值是1/|x-y|。因此,一個質量分布μ的引力場在x的牛頓位勢是:

1772年,拉普拉斯(Laplace,P.-S.)證明了,在不分布質量的地方,位勢滿足拉普拉斯方程。這樣,物理問題便化為求解偏微分方程的數學問題。
從18世紀到19世紀末,位勢論的研究限於n維歐氏空間上的牛頓位勢(n≥3)和對數位勢(n=2),即所謂經典位勢論。其中心問題之一是古典狄利克雷問題的求解。1823年,泊松(Poisson,S.-D.)就球域情形給出了解的積分公式;1828年,格林(Green,G.)對邊界充分光滑的有界區域,從物理直觀出發並藉助于格林函式給出了解;1840年,高斯(Gauss,C.F.)採用變分法解決了平衡問題並得出狄氏問題的新解法。這兩個問題與掃除問題相關聯,此後一直被稱為位勢論三大基本問題。1855年,狄利克雷(Dirichlet,P.G.L.)和黎曼(Riemann,(G.F.)B.)利用所謂狄利克雷原理給出了解。此外,還有龐加萊(Poincaré,(J.-)H.)的掃除法,施瓦茲(Schwarz,H.A.)的交錯法等。但是,由於缺乏足夠的數學工具,這些解法是不嚴密的,需要附加條件。另外,在這一時期的主要成果還有:1839年,埃恩蘇(Earnshaw,E.)證明狄氏解的極值原理;1850年,黎曼把位勢論與函式論作統一處理,揭示了格林函式和位勢同保形映射之間的密切聯繫;1886年,哈納克(Harnack,C.G.A.)建立哈納克不等式及哈納克收斂原理。此外,關於諾伊曼問題及多重調和函式的研究也有不少成果。這樣,直到19世紀末,位勢論的三個基本原理,即極小值原理、收斂性質及狄利克雷問題的可解性已基本建立,它為現代位勢論的發展作了很好的準備。
核
核是位勢論的基本概念。在位勢論中,所謂核,常指一般位勢的核。這時若K(x,y)≥0恆成立,則稱K為正核;令K′(x,y)=K(y,x)(K′稱為K的轉置核),若K′=K,則稱K為對稱核;當Ω為阿貝爾群且有K(x,y)=K(x-y)時,則稱K為平移不變核;若對於任意有緊支集的μ,有:
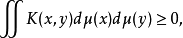
歸納法
從個別的或特殊的經驗事實出發而概括得出一般性原理、原則的思維方法。主要包括完全歸納法、枚舉歸納法、排除歸納法(求因果五法)以及觀察、實驗、比較、分類、分析、綜合、統計中選樣、求平均數等收集和整理材料的方法。在傳統邏輯中,有時亦用作歸納推理的別名,即對歸納法與歸納推理不作明確區分,等同使用。關於歸納法的某些理論問題,早在古希臘亞里士多德的著作中就已經有所涉及,但只是隨著近代實驗自然科學的產生,對歸納法的研究和運用才逐漸得到了重視。17世紀的培根,最早系統研究了歸納法學說。他提出要創立一種真正的歸納法。這種歸納法應當是能夠發現構成事物的簡單性質和形式,即事物原因的一種發明的方法、發現的方法。為此,他既批評了被經院主義化了的亞里士多德的演繹法,也批評了那種從感覺材料一下子就飛到最高的普遍原則上去的簡單枚舉的歸納法。認為這種歸納法“是很幼稚的;其結論是不穩定的,大有從相反事例遭到攻襲的危險”。他認為“對於科學的發現和論證真正有用的歸納法,必須以正當的排拒法和排除法來分析自然,有了足夠數量的反面事例,然後再得出根據正面事例的結論”(同上)。這就在邏輯史上第一次提出了以求得現象原因為目標的排除歸納法。在F.培根以後,一些科學家或哲學家,如伽利略、牛頓、赫舍爾、休厄爾等人對歸納法的發展曾作出過不同程度的貢獻。J. S.穆勒則將F.培根開始提出的排除歸納法進一步系統化,提出了著名的求因果五法。隨著歸納法的發展及在實驗自然科學中的廣泛運用,歷史上的某些哲學家和邏輯學家,曾不適當地過分誇大了歸納法的作用,而陷入歸納萬能論錯誤。具有這種觀點的人認為,歸納法是萬能的,是不會犯錯誤的,是惟一正確的科學方法。他們否認演繹法在科學發現和科學理論形成過程中的作用,割裂了歸納法與演繹法不可分割的聯繫。事實上,歸納法與演繹法是相互聯繫、相互依賴、相互滲透的。任何歸納法的運用,都離不開一般性理論知識的指導,因而都是以演繹活動為其前導的;在獲得新的一般性知識的過程中,單靠歸納法是不能證明其必然性的;而且,歸納法所據以獲得一般性知識的結論的依據是經驗,而經驗總是未完成的,歸納法不可能是萬能的。恩格斯指出:“我們用世界上的一切歸納法都永遠做不到把歸納過程弄清楚。只有對這個過程的分析才能做到這一點。”
