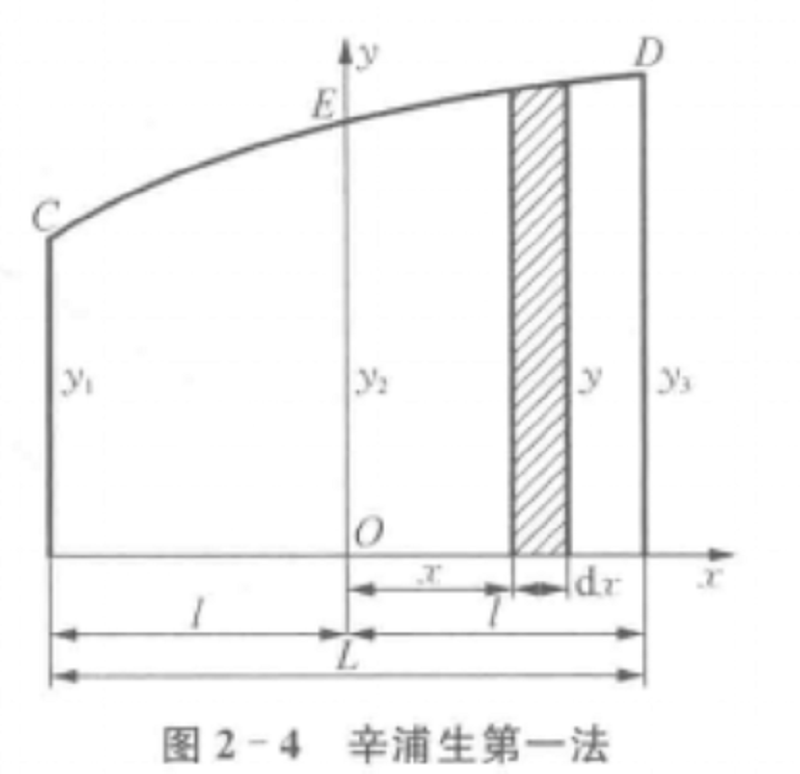
辛浦生法也稱拋物線法,是採用等分間距,以若干段二次或三次拋物線近似代替實際曲線,計算各段拋物線下面積的數值積分法。船體的大部分曲線實際上是與拋物線相近,套用此方法進行船體計算所得的結果在工程上具有足夠精確,故得到廣泛套用。以二次拋物線近似代替實際曲線的計算方法稱為辛浦生第一法,以三次拋物線近似代替實際曲線的計算方法稱為辛浦生第二法,在實際計算中,多採用辛浦生第一法。
基本介紹
- 中文名：辛浦生法
- 外文名：Symplectic method
- 別稱：拋物線法
辛浦生第一法,
辛浦生第一法
如概述圖所示,設曲線CD為船體上的某一段曲線,取等間距為1的三個縱坐標,其值為y1,y2,y3。求其曲線下的面積A。為方便起見,將原點選在曲線底邊邊長為2l的中點。假定該曲線用二次拋物線表示,其方程為
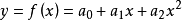
式中,a0,a1,a2為常數。則曲線下的面積將由定積分公式給出:
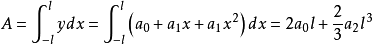
同時,取面積表達式為：
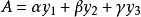
令二次拋物線通過曲線上對應於等分點C,E,D三點,則得：
當x=-l時：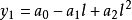
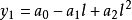
當x=0時：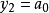
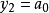
當x=+l時：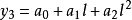
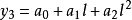
解上述方程組,可得：
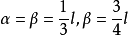
令L為曲線底邊長,L=21,則上式可寫成：
式中,括弧內各縱坐標值前的係數[1,4,1]為辛氏乘數(SM),括弧前分數的分子為曲線底邊邊長,分母恰等於括弧內辛氏乘數之和,通常記作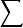
SM,上式用於船體計算時,稱為辛浦生第一法,又稱為辛浦生[1,4,1]法。
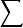
必須指出,只有當曲線底邊的等分數目為偶數時(即縱坐標數目為奇數),方可採用辛浦生第一法。
