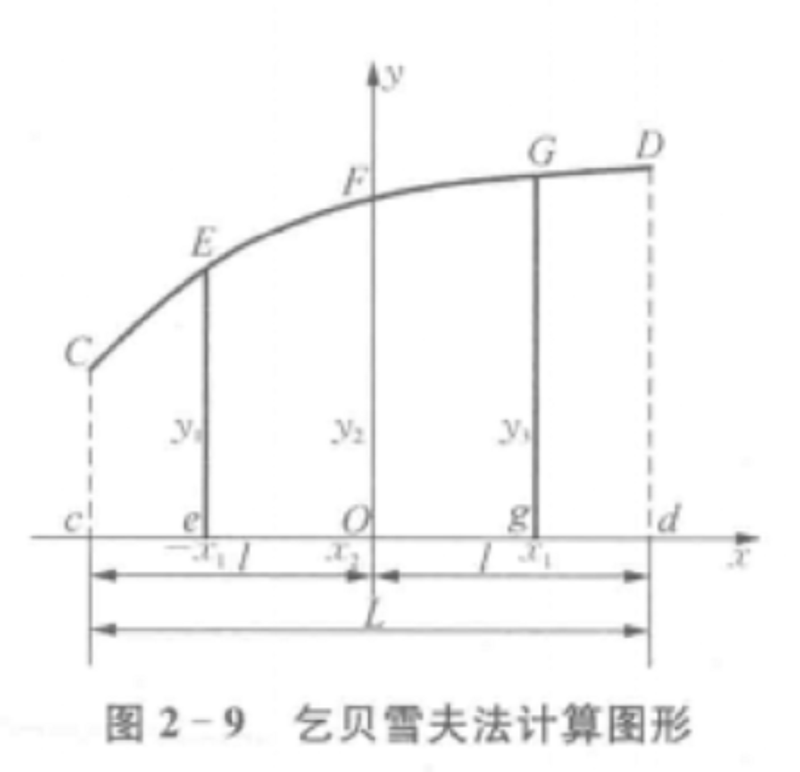
一種採用n個特定位置的不等間距坐標,以n次拋物線近似代替實際曲線,以計算該曲線下一定區域內面積的數值積分法。
基本介紹
- 中文名:乞貝雪夫法
- 外文名:Tchebysheff's rule
- 類型:數值積分法
基本概念,乞貝雪夫法套用,
基本概念
梯形法和辛浦生法,都是採用等間距的縱坐標值乘上不同的係數相加,即得所求曲線下的面積。能否找到一個方法,即套用不等間距的各縱坐標值之和,再乘上一個共同的係數來得到曲線下的面積。乞貝雪夫就是基於這個思想,用n次拋物線代替實際曲線,採用不等間距的n個縱坐標計算該拋物線下在給定區間的面積,以此近似地代替曲線下的面積,這時曲線下面積A為n個縱坐標值之和,再乘上一個共同係數p。p值為曲線底邊邊長L除以縱坐標數目n,即p=L/n,則

如果曲線CD用9次拋物線替代,其9個縱坐標位置如圖1所示。乞貝雪夫法的各縱坐標對稱於原點布置,其數學分析可歸結為尋找各個縱坐標距原點的距離和共同係數p,如各縱坐標位置已確定,則可在曲線圖形上量得各縱坐標的數值,相加後再乘上一個共同係數,即得到曲線CD下的面積。由於所取的縱坐標數目不同,其相應的位置亦不同。
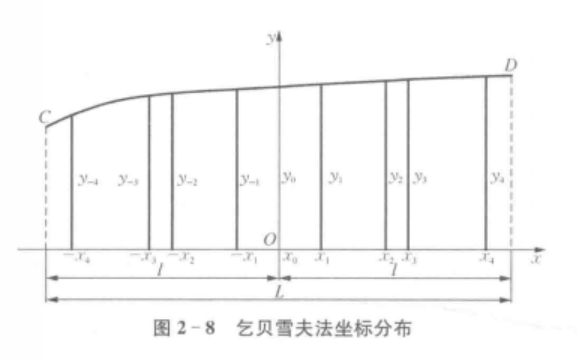 乞貝雪夫法坐標分布
乞貝雪夫法坐標分布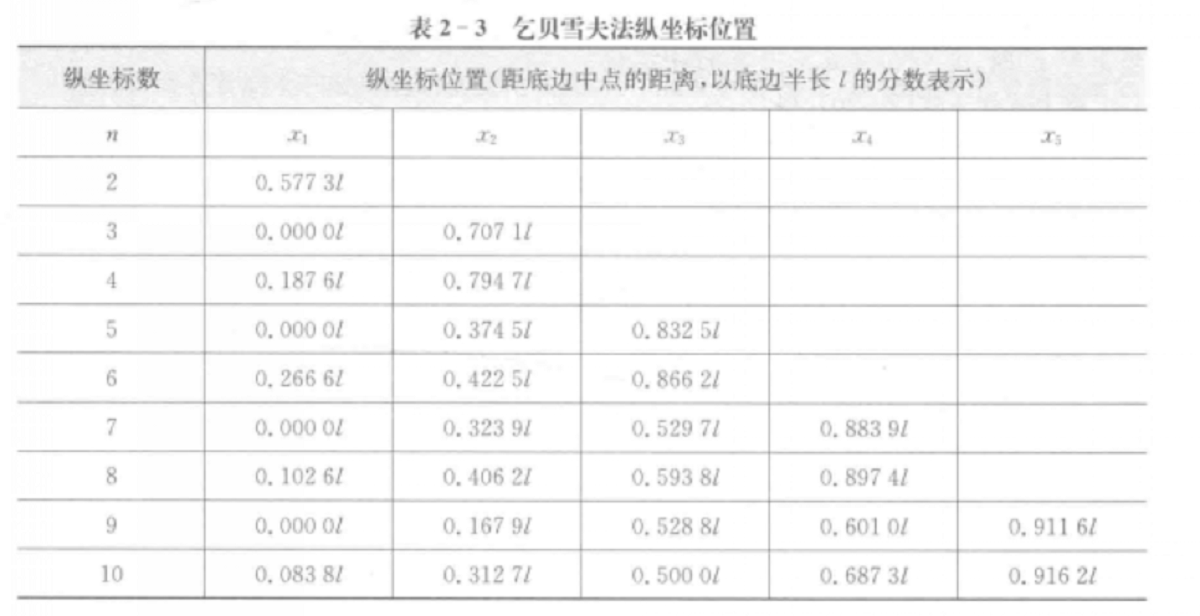 圖1:乞貝雪夫法縱坐標位置圖
圖1:乞貝雪夫法縱坐標位置圖推導三個坐標的乞貝雪夫法。如圖2所示,已知曲線CD及其底邊長度L,現取個縱坐標,其值為y1,y2及y3,坐標原點取在曲線底邊cd的中點O。取曲線CD下面積的表達式為:

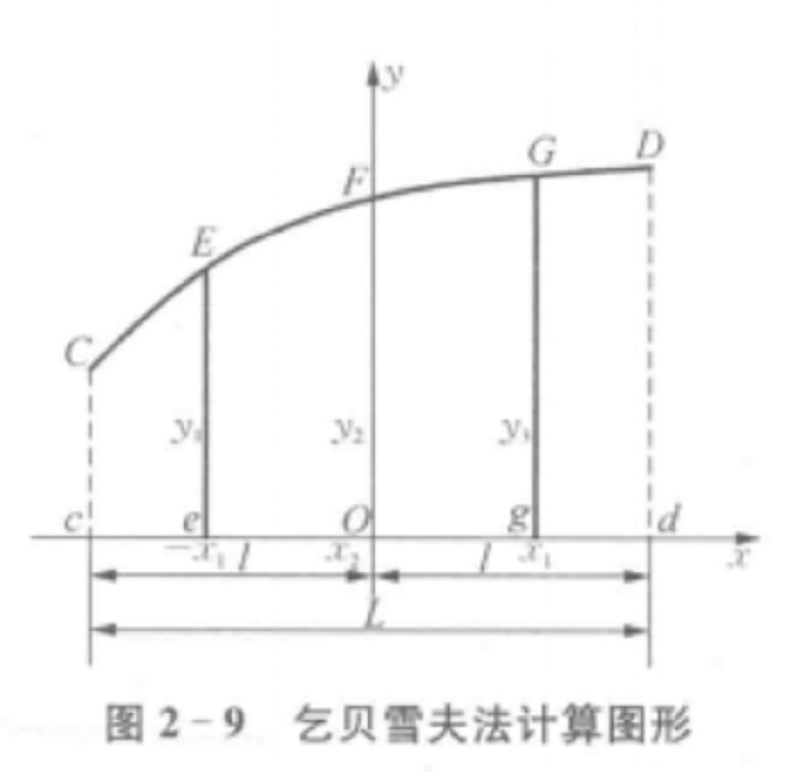 圖2
圖2為了確定上式中三個縱坐標的位置(其中y2在坐標原點處)和一個共同係數p,假定曲線CD用三次拋物線方程替代,即

式中,a0,a1,a2,a3為常數,則曲線CD下的面積將由定積分公式給出

所設三次拋物線必須通過各縱坐標與曲線CD相交的E,F,G三點,即
當x=-x1時, (3)
(3)

當x=-x0時, (4)
(4)

當x=x1時, (5)
(5)

將(3)、(4)、(5)代入(1)得

由於式(2)與式(6)代表同一面積,故兩式a0,a1中各項係數應分別相等,即

解方程組,得


上式結果說明,在離曲線CD的底邊中點為±0.7071l(l為曲線CD的半長)處,設立兩個縱坐標eE及gG,並量取它們的數值和中點處縱坐標OF的數值,然後將三個縱坐標的數值相加,再乘以共同係數2/3l,即得曲線CD的面積。

上式是三坐標的乞貝雪夫法,式中括弧內為各縱坐標值的總和,括弧外為共同係數,其分子為曲線底邊的總長度,即cd=L=2L;分母為所取的縱坐標數目n。
同理,可推導出縱坐標數目n為2,3,4,5,6,7,8,9和10時的縱坐標位置,其曲線下面積的一般表達式為

為了保證計算的精確性,在船舶靜力學計算中一般採用9個以上的縱坐標數。用乞貝雪夫法進行船體計算時,需要繪製乞貝雪夫橫剖面圖,且讀取縱坐標數值比較繁瑣,不如梯形法、辛浦生法等方便,因此僅在手工計算大傾角穩性時套用,該方法也可以用做計算靜矩和慣性矩等。
乞貝雪夫法套用
為了求得船體的各種性能,必須計算船體的一些截面積,面積重心以及排水體積,體積重心等。但由於船體形狀複雜,難以用解析法獲得,通常用近似計算方法來進行。常用的計算方法是數值積分法,如梯形法,辛浦生法和乞貝雪夫法等。這些近似計算法可用於手算,而且也是電算的基礎。