將行列式D行的項轉為列的項成為行列式DT
則行列式DT稱為行列式D的轉置行列式
即行列式D行與列對換得到的新行列式DT
例如D第一行為a11、a12、a13···a1n
而DT第一行為a11、a21、a31···an1
基本介紹
- 中文名:轉置行列式
- 外文名:transposed determinant
- 所屬學科:數學
- 相關詞條:轉置矩陣
性質
用途
證明

































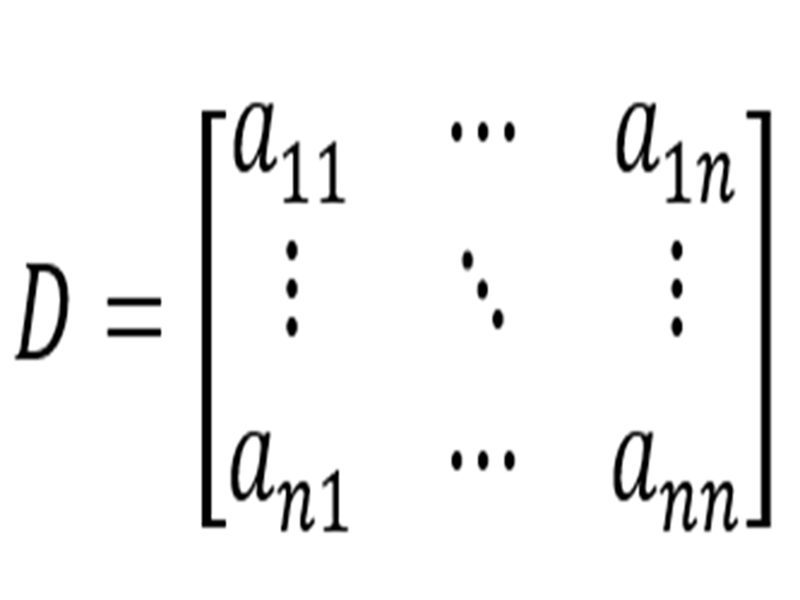
將行列式D行的項轉為列的項成為行列式DT
則行列式DT稱為行列式D的轉置行列式
即行列式D行與列對換得到的新行列式DT
例如D第一行為a11、a12、a13···a1n
而DT第一行為a11、a21、a31···an1

































將行列式D行的項轉為列的項成為行列式DT則行列式DT稱為行列式D的轉置行列式即行列式D行與列對換得到的新行列式DT例如D第一行為a11、a12、a13···a1n而DT第一行為a11、a21、a31···an1性質行列式...
①行列式A中某行(或列)用同一數k乘,其結果等於kA。②行列式A等於其轉置行列式A(A的第i行為A的第i列)。③若n階行列式|α|中某行(或列);行列式則|α|是兩個行列式的和,這兩個行列式的第i行(或列),一個是b₁,b₂,…,bₙ;另一個是с₁,с₂,…,сₙ;其餘各行(或列)上的元與|...
定義 把 矩陣 的行列互換之後得到的矩陣,稱為 的轉置矩陣,記作 ,即 由定義可知, 為 矩陣,則 為 矩陣。例如,,。如果 階方陣和它的轉置相等 ,即 ,則稱矩陣 為對稱矩陣。如果 ,則稱矩陣 為反對稱矩陣。運算性質 (1);(2);(3);(4);(5),即轉置矩陣的行列式不變。
主對角線下方元素全為零的行列式,也即非零元素只出現在主對角線及上方的行列式,稱為上三角形行列式(當i>j時, )。對上三角形行列式也總有:證明:行列式及其餘子式均依次按第一行展開即得(或因為上三角形行列式與下三角形行列式互為轉置行列式)。對角形行列式 主對角形行列式:主對角線上方、下方的元素全為零...
將行列式的行列互換,行列式的值不變,其中行列互換相當於轉置。這個性質可以簡單地記作 例如: 行列式的乘法定理:方塊矩陣的乘積的行列式等於行列式的乘積。 特別的,若將矩陣中的每一行每一列上的數都乘以一個常數r,那么所得到的行列式不是原來的r倍,而是rⁿ倍。·以上的乘法公式還可以進一步推廣為所謂柯...
稱為對角形行列式,亦稱對角行列式。它既是一個上三角形行列式,又是一個下三角形行列式。行列式的七條性質 1. 行列式D與它的轉置行列式相等。2. 互換行列式的兩行(列),行列式的值改變符號。由性質2可得出:如果行列式有兩行(列)的對應元素相同或成比例,則這個行列式為零。3. n階行列式等於任意一行(列)的所有...
性質1 行列式與它的轉置行列式相等。性質2 互換行列式的兩行(列),行列式變號。推論 如果行列式有兩行(列)完全相同,則此行列式為零。性質3 行列式的某一行(列)中所有的元素都乘以同一數k,等於用數k乘此行列式。推論 行列式中某一行(列)的所有元素的公因子可以提到行列式符號的外面。性質4 行列式中如果有...
矩陣行列式是指矩陣的全部元素構成的行列式,設A=(a)是數域P上的一個n階矩陣,則所有A=(a)中的元素組成的行列式稱為矩陣A的行列式,記為|A|或det(A)。若A,B是數域P上的兩個n階矩陣,k是P中的任一個數,則|AB|=|A||B|,|kA|=kⁿ|A|,|A*|=|A|,其中A*是A的伴隨矩陣;若A是可逆矩陣,...
(1)行列式在基本行操作下是不變的;(2)本體行列式是1;(3)如果一行在R中乘以a,則行列式左乘以a;(4)行列式乘法:det(AB)= det(A)det(B);(5)如果交換兩行,行列式乘以-1;(6)如果R是可交換的,那么行列式轉置之後是不變的。Tannaka–Artin問題 假設K在其中心F是有限的,縮小的範數給出...
行列式初等變換 相關性質 性質1:行列互換(即轉置),行列式不變。性質2:一數乘行列式的一行就相當於這個數乘此行列式 性質3:如果行列式中有兩行相同,那么行列式為0,所謂兩行相同,即兩行對應的元素都相等 性質4:如果行列式中,兩行成比例,那么該行列式為0 性質5:把一行的倍數加到另一行,行列式不變 性質...
1.4.1 轉置行列式 1.4.2 行線性性 1.4.3 行列式的初等變換 §1.5 Laplace定理 1.5.1 子式·餘子式·代數餘子式 1.5.2 Laplace定理 1.5.3 行列式的按行展開與按列展開 1.5.4 方陣乘積的行列式 §1.6 行列式的計算 1.6.1 三角化 1.6.2 降階法與鑲邊法 1.6.3 歸納與遞推 §1.7 ...
第1章 行列式 1.1 預備知識 1.1.1 排列及其逆序數 1.1.2 數域的基本概念 1.2 n階行列式的定義 1.2.1 二、三階行列式 1.2.2 n階行列式的定義 1.3 行列式的性質 1.3.1 行列式的另外表示及行列式的轉置 1.3.2 行列式的性質 1.4 行列式按一行(列)展開 1.4....
§1.3 行列式的性質與計算 一、對換 二、行列式的性質 三、行列式的計算 §1.4 行列式按行(列)展開 §1.5 克萊姆法則 習題一 第二章 矩陣及其初等變換 §2.1 矩陣的定義 一、矩陣的基本概念 二、幾種特殊類型的矩陣 §2.2 矩陣的運算 一、矩陣的線性運算 二、矩陣的乘法 三、矩陣的轉置 四、方陣的...
第一章 行列式 § 1.1 行列式的定義 § 1.2 行列式的性質 § 1.3 Cramer 法則 § 1.4 行列式按行展開與轉置 § 1.5 行列式的計算 § 1.6 行列式的等價定義 § 1.7 Laplace定理 第二章 矩陣 § 2.1 矩陣的概念 § 2.2 矩陣的運算 § 2.3 方陣的逆陣 § 2.4 矩陣的初等變換與初等矩陣 §...
1.2.1 二、三階行列式 1.2.2 n階行列式的定義 1.3 行列式的性質 1.4 行列式按行(列)展開 1.5 克拉默法則 習題1 第2章 矩陣 2.1 矩陣的概念 2.1.1 矩陣的定義 2.1.2 幾種特殊的矩陣 2.2 矩陣的運算 2.2.1 矩陣的加法與數乘 2.2.2 矩陣的乘法 2.2.3 矩陣的轉置 2.2.4 方陣的...
2.2.4 矩陣的轉置(34)2.2.5 方陣的行列式(36)2.2.6 共軛矩陣(37)2.3 逆矩陣(37)2.4 矩陣分塊法(39)2.4.1 分塊矩陣的概念(40)2.4.2 分塊矩陣的運算(40)習題2(43)第3章 矩陣的初等變換與線性方程組(46)3.1 矩陣的初等變換(46)3.1.1 矩陣初等變換的引入(46)3.1.2...
矩陣212矩陣的加法213數乘矩陣214矩陣與矩陣的乘法215方陣的冪運算216矩陣的轉置217共軛矩陣〖〗背景聚焦:天氣的馬爾可夫(Markov)鏈習題2122幾種特殊的矩陣221對角矩陣、數量矩陣和單位矩陣222上(下)三角形矩陣223對稱矩陣和反對稱矩陣224冪零...
2.1.5 矩陣的轉置 (41)2.1.6 方陣的行列式 (42)習題2.1 (44)2.2 逆矩陣 (46)2.2.1 逆矩陣的概念 (46)2.2.2 逆矩陣的性質 (47)2.2.3 矩陣可逆的判定與逆矩陣的求法 (47)習題2.2 (52)2.3 分塊矩陣 (52)2.3.1 分塊矩陣的加法 (53)2.3.2 分塊矩陣的乘法...
1.2.2 行列式的計算11 *1.2.3 拉普拉斯定理18 1.3 克拉默法則20 習題124 第2章 矩陣28 2.1 矩陣的概念28 2.1.1 引例28 2.1.2 矩陣的概念29 2.1.3 幾種特殊的矩陣31 2.2 矩陣的運算33 2.2.1 矩陣加法33 2.2.2 數乘矩陣34 2.2.3 矩陣乘法35 2.2.4 矩陣的轉置39 2.2.5 方陣的...
1.2.4 矩陣的轉置 1.3 可逆矩陣 1.3.1 可逆矩陣的定義 1.3.2 可逆矩陣的性質 1.4 分塊矩陣 1.4.1 分塊矩陣的定義 1.4.2 分塊矩陣的運算 1.5 MATLAB軟體的套用 1.5.1 輸入矩陣 1.5.2 矩陣的運算 本章知識結構與內容提要 習題一 第二章 矩陣的初等變換 2.1 高斯消元法 2...
1.3行列式的性質 1.4克拉默法則 1.5套用舉例 1.5.1用二階行列式求平行四邊形的面積 1.5.2用三階行列式求平行六面體的體積 習題一 實驗練習一 第2章矩陣及其運算 2.1矩陣的定義 2.1.1引例 2.1.2定義 2.2矩陣的運算 2.2.1矩陣的線性運算 2.2.2矩陣的乘法運算 2.2.3轉置 2.2.4方陣的行列式 ...
1.2.1 二、三階行列式 1.2.2 n階行列式的定義 1.3 行列式的性質 1.4 行列式按行(列)展開 1.5 克拉默法則 習題1 第2章 矩陣及其運算 2.1 矩陣的概念 2.1.1 矩陣的定義 2.1.2 幾種特殊的矩陣 2.2 矩陣的運算 2.2.1 矩陣的加法與數乘 2.2.2 矩陣的乘法 2.2.3 矩陣的轉置 2.2.4 ...
1.4行列式按行(列)展開12 1.4.1行列式按某一行(列)展開12 *1.4.2 行列式按某k行(列)展開16 1.5克萊姆法則17 習題122 第2章矩陣28 2.1矩陣的概念28 2.1.1矩陣的概念28 2.1.2常用的特殊矩陣29 2.2矩陣的運算30 2.2.1矩陣的加法和數乘30 2.2.2矩陣的乘法32 2.2.3矩陣的轉置38 2....
第1章行列式 1.1二階與三階行列式 1.2n階行列式的定義 1.3n階行列式的性質 1.4n階行列式的計算 1.5克萊姆(Cramer)法則 習題一 第2章矩陣 2.1矩陣的概念及線性運算 2.2矩陣的乘法 2.3矩陣的轉置和對稱矩陣 2.4可逆矩陣 2.5矩陣的初等變換和初等矩陣 2.6矩陣的秩 2.7分塊矩陣 習題二 第3章向量...
1.3.5將行列式拆成兩個行列式之和(積)計算 1.3.6用遞推法計算 1.3.7用數學歸納法 1.4克拉默法則 1.5行列式的軟體求解 1.5.1基本命令 1.5.2求解示例 習題1 第2章矩陣 2.1矩陣的概念 2.2矩陣的運算 2.2.1矩陣的加法 2.2.2數與矩陣相乘 2.2.3矩陣與矩陣相乘 2.2.4矩陣的轉置 2.2.5...
§1.5范德蒙德行列式和拉普拉斯 定理 一、 范德蒙德行列式 二、 拉普拉斯定理及其結論 習題1.5 §1.6克拉默法則 習題1.6 §1.7綜合例題 總習題一 第二章矩陣及其運算 §2.1矩陣的運算 一、 矩陣的加法 二、 數和矩陣的乘法 三、 矩陣的乘法 四、 矩陣的冪 五、 矩陣的轉置 習題2.1 §2.2可逆矩陣 ...
三、n階行列式的定義 §1.2 行列式的基本性質 §1.3 行列式按一行(列)展開 §1.4 克萊姆法則 背景資料(1)習題一 第二章 矩陣 §2.1 矩陣的概念 一、矩陣的定義 二、幾種特殊的矩陣 §2.2 矩陣的基本運算 一、矩陣的加減法 二、矩陣的數乘 三、矩陣乘法 四、矩陣的轉置 五、方陣的行列式 六、...
