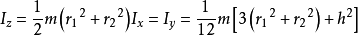基本介紹
- 中文名:轉動慣量列表
- 外文名:Moment of inertia list
- 描述:常見物理模型的轉動慣量
- 學科:力學
- 領域:力學
- 相關術語:截面慣量
簡介,常見物理模型的轉動慣量,相關術語,
簡介
值得注意的是,不應將其與截面慣量(又稱截面二次軸矩(second axial moment of area),截面矩(area moment of inertia)混淆,後者用於彎折方面的計算。以下之轉動慣量假設了整個物體具有均勻的常數密度。
常見物理模型的轉動慣量
| 描述 | 轉動慣量 | 註解 |
|---|---|---|
兩端開通的薄圓柱殼, 半徑為r,質量為m | 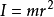 | 此表示法假設了殼的厚度可以忽略不計。此為下一個物體,當其r1=r2時的特例。 |
兩端開通的厚圓柱, 內半徑r1,外半徑r2, 高h,質量m | — | |
實心圓柱, 半徑為r,高h, 質量m |   | 此為前面物體,當其r1=0時的特例。 |
薄圓盤,半徑為r, 質量m |  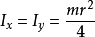 | 此為前面物體,當其h=0時的特例。 |
圓環,半徑為r, 質量m |  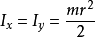 | 此為後面環面,當其b=0時的特例。 |
實心球,半徑為r, 質量m |  | — |
空心球,半徑為r, 質量m |  | — |
圓錐,半徑為r,高h, 質量m |   | — |
實心長方體,高h, 寬w,長d,質量m |    | 邊長為 s的立方體的轉動慣量 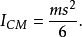 |
細棒,長L,質量m | 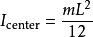 | 此表示法假設了棒的寬度和厚度可以忽略不計。此為前面物體,當其w=L,h=d=0時的特例。 |
細棒,長L,質量m |  | 此表示法假設了棒的寬度和厚度可以忽略不計。 |
環面,圓管的半徑a, 截面的半徑b,質量m。 | 關於直徑:  關於縱軸:  | — |
薄多邊形,質量m。 |  | — |
相關術語
- 截面慣量列表
- 慣量張量列表