軸對稱空間課題

軸對稱空間課題也稱軸對稱彈性空間課題，是近代土力學理論的一次重要發展。其解決了彈性半空間體在軸對稱荷載下應力和位移計算的某些數值解。

基本介紹

• 中文名：軸對稱空間課題
• 外文名：Axisymmetric space problem
• 學科：土力學
• 貢獻者：K.Terasawa（寺澤寬一）

定義

在1885年，布辛尼斯克對彈性均質半空間體作出的研究的基礎上，1916年日本學者寺澤寬一對在軸對稱荷載下的半空間體，採用貝塞爾函式法求得了應力和位移計算的完整表達式，對於一些特殊點，還可簡化為收斂迅速的無限級數，從而獲得半空間體在軸對稱荷載下應力和位移計算的某些數值解。1929年洛夫（A.E.H.Love）採用勢能法又做出了後續的研究貢獻。

貝塞爾

性質

彈性層狀半空間體在外荷載作用下的應力、變形和位移分析，屬於空間課題。在空間課題中，如果彈性體的幾何形狀，約束條件以及所受的外荷載因素，都對稱於某一軸，則所有的應力、變形和位移也就對稱於這一軸，這類問題稱之為軸對稱空間課題。由於彈性層狀體系在水平向和垂直向都是無限的，因而其結構本身一定對稱於某一軸，如果荷載也是軸對稱荷載，則該課題必定為軸對稱空間課題。

布辛尼斯克

內容

1.軸對稱空間坐標系

首先建立一個三維的柱坐標系並取一六面體微元，如圖1所示

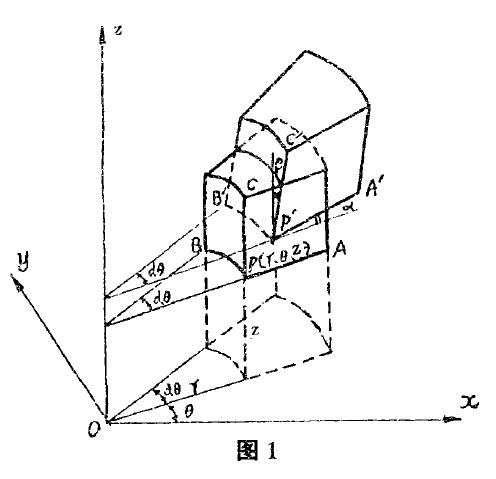
圖1

通過對徑向力取平衡可以得到軸對稱空間課題的平衡微分方程（推導略）：

其中 ，從上式可以看出，兩個方程共有四個未知量，未知量的個數多於方程的個數，所以只由靜力學來考慮問題，不足以解得上述四個應力分量。只有研究物體變形及其與應力的聯繫，才能得到所缺少的方程。

2.變形連續方程

為了解決上面提到的缺少必要方程無法解出四個應力分量的問題，又有很多科學家對此進行了理論研究。

聖維南

聖維南（B.de Saint-Venant）於1864年提出研究物體的變形時，從物體內割出一些圓柱微分單元體，顯然，各相鄰單元體的變形應是諧調的，所以物體在變形前是一個連續體，變形後也是一個連續體。

如圖2所示六面體微元發生一徑向微位移u，軸向微位移w

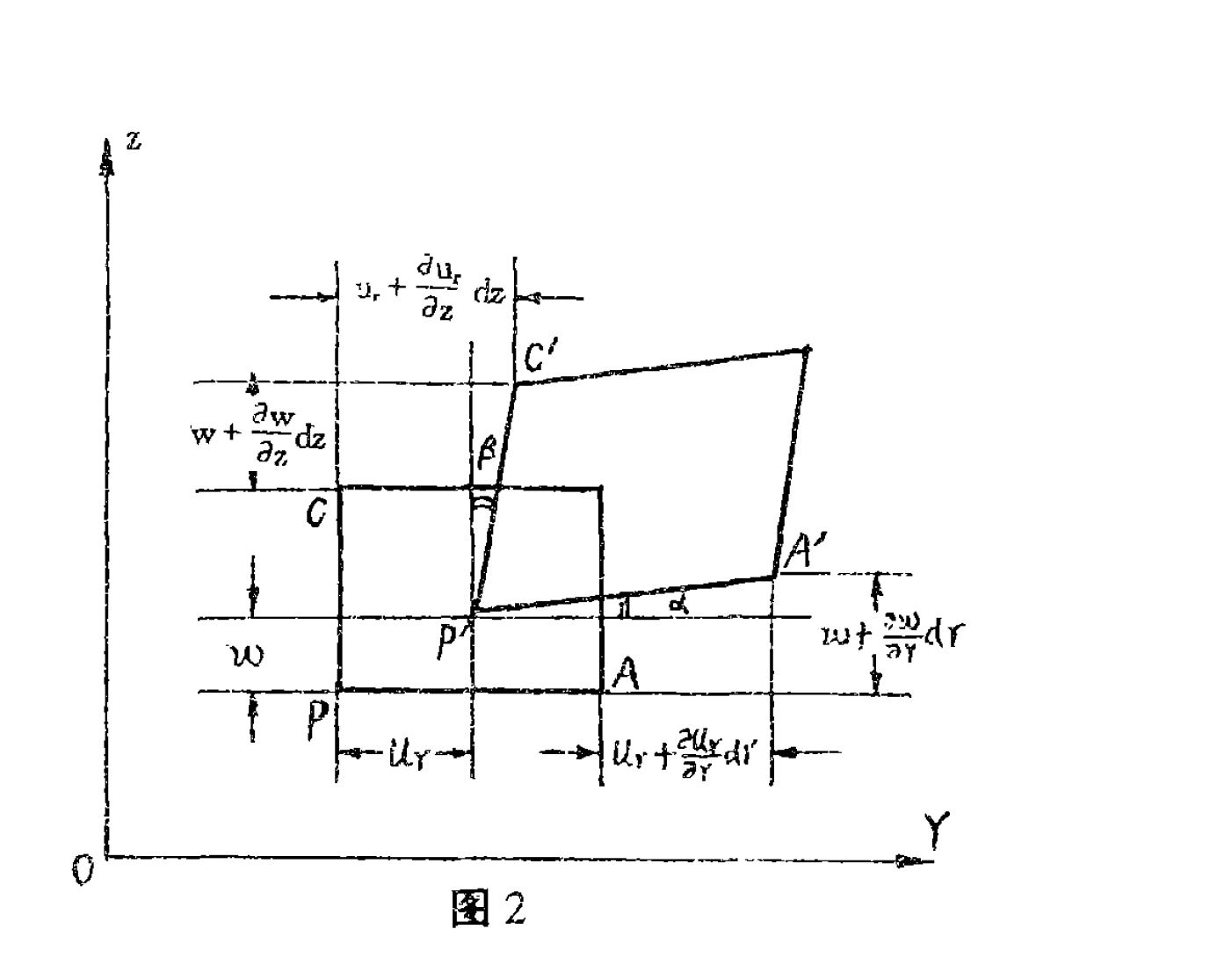
圖2

得到用應力表示的變形連續方程（推導略）：

式中：

I₁為第一應力不變數；

▽為軸對稱空間課題的拉普拉斯運算元。

上述求解應力分量解析解在實際情況下十分困難，一般採用應力函式求解。應力函式法求解又分洛夫（A.E.H.Love）法和蘇斯威爾法。

3.洛夫（A.E.H.Love）法

設應力函式 並給定：

將上式代入平微分方程和變形連續方程，除平衡微分方程第一個恆等於0外，其餘皆轉化為重調和方程：

後續又可採用分離變數法和漢克爾積分變換法求解。

最後得到四個應力分量的表達式如下：

兩個位移分量：

式中：

只要根據邊界條件和層間結合條件求得A、B、C、D就能獲得該課題的全部精確解。

4.蘇斯威爾（Southwell）法

與洛夫法十分相似，蘇斯威爾法是給定位移條件，並代入物理方程，間接得到洛夫法中直接給定的應力微分方程。

同理代入平微分方程和變形連續方程，最後得到：

式中

後續也是採用漢克爾積分變換法求解。

最後得到四個應力分量的表達式如下：

兩個位移分量：

式中：

只要根據邊界條件和層間結合條件求得A、B、C、D就能獲得該課題的全部精確解。

優缺點

用蘇斯威爾法求解應力與位移分量的一般表達式，要比洛夫法簡捷些。但蘇斯威爾法目前尚未找到向非軸對稱空間課題推廣的途徑，而洛夫法卻易於向非軸對稱課題推廣。

套用

在交通運輸工程中的道路建設領域是一次重要發展，根據汽車在公路上運動狀態的受力分析，一般情況下，作用有垂直荷載和單向水平荷載。對於垂直荷載，長期以來（在當時）都把它化為相當的圓形軸對稱荷載（如圓形均布荷載、半球形荷載等）來研究。因此，彈性層狀體系在圓形垂直荷載作用下的應力、變形和位移分析，可歸結為軸對稱空間課題。至於單向水平荷載，屬於非軸對稱荷載，但在後來的研究中已經解決了該問題，這裡只做軸對稱問題的介紹。