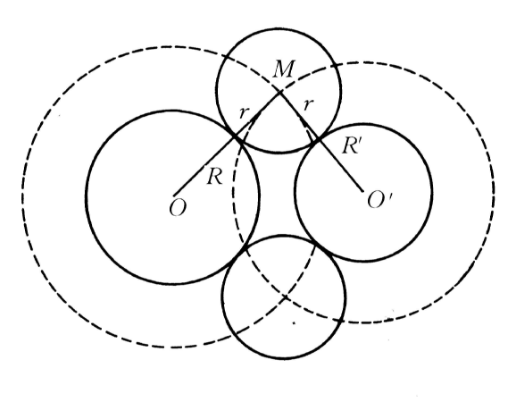
如果解決一個作圖題歸結起來是要確定某一個點的位置,可以暫時放棄這點所應滿足的條件之一,這時滿足其餘條件的點可形成一個軌跡;再改換放棄另一個條件,又得到一個軌跡,所求的點應在這兩個軌跡上,因此,兩個軌跡的交點就是所求作的點,像這樣利用軌跡的交點來解作圖題的方法,叫做軌跡交點法或軌跡交接法或徑稱軌跡法。
基本介紹
- 中文名:軌跡交點法
- 外文名:method of intersection point of locus
- 所屬學科:數學
- 所屬問題:平面幾何(尺規作圖)
- 別稱:軌跡交接法或徑稱軌跡法等
基本介紹,例題解析,
基本介紹
軌跡交點法(method of intersection point of locus)是解作圖題的一種重要方法,解作圖題常歸結到確定某一點的位置,如果這個點的位置是由兩個條件確定的,先放棄其中一個條件,那么這個點的位置就不定而形成一個軌跡;若改換放棄另一個條件,這個點就在另一個軌跡上,故此點便是兩個軌跡的交點,這種利用軌跡的交點來解作圖題的方法稱為軌跡交點法,或稱為交軌法、軌跡交截法、軌跡法。用這種方法來作圖,稱為軌跡法作圖。
例如,設⊙O與⊙O′相離,半徑分別為R與R′,求作半徑為r的圓,使其與⊙O及⊙O′外切,該作圖題的思路要點是:設⊙M是合條件的圓,即其半徑為r並與⊙O及⊙O′外切(如圖1),顯然,M點是由兩個軌跡確定的,即M點既在以O為圓心以R+r為半徑的圓上,又在以O′為圓心以R′+r為半徑的圓上,因而所求圓的圓心位置可確定,於是該作圖題可以求解。若⊙O與⊙O′相距為b,當2r<b時,該題無解;當2r=b時,有惟一解;當2r>b時,有兩解。
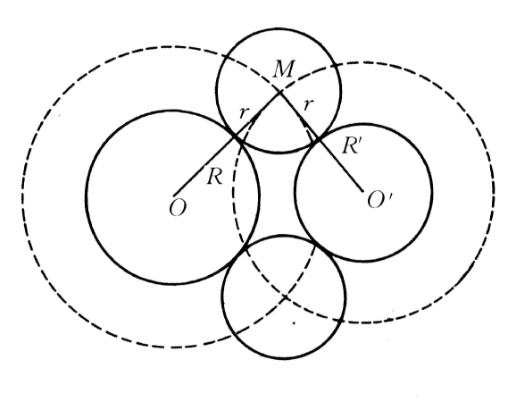 圖1
圖1軌跡交點法在作圖中套用廣泛,凡屬作圖,幾乎沒有不用到它的。這是因為我們所使用的工具——直尺和圓規的作圖在本質上就體現了求軌跡交點的作用。正因如此,軌跡交點法可說就是其他作圖方法的基礎。
有時欲確定的某一個點已明確指出系在某已知圖形上,那么只要求出一個軌跡就可以了,這種情形叫做單軌法。如果並未指出在某已知圖形上,需要求出兩個軌跡才能確定所求點的位置,這種情形叫做雙軌法。
能確定某一個點的軌跡常常有若干個,為使作圖簡捷,我們應該注意選擇那些便於作出的軌跡。
例題解析
【例1】 已知一邊及這邊上的中線和高,作三角形。
已知:線段a、m、h,求作:△ABC,使BC=a,中線AD=m,高AE=h。
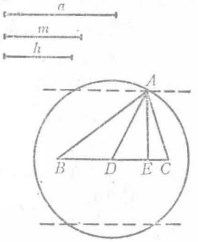 圖2
圖2分析:假設△ABC已作出,其中BC=a,中線AD=m,高AE=h,BC=a,如果A點可定,這個作圖題就可解,A點適合兩個條件:1.和BC的中點的距離等於m;2.和BC的距離等於h。若利用第一個條件,先放棄第二個條件,可得以BC的中點為圓心,m為半徑的圓;再利用第二個條件而放棄第一個條件,得出僅適合於第二個條件的點的軌跡,是和BC平行且距離等於h的兩條直線。所求的A點就是這兩個軌跡的交點(圖2)。
作法:
1.作BC=a。
2.取BC的中點D,以D為圓心,m為半徑作圓。
3.作和BC平行並且距離等於h的直線交圓於A。
4.連結AB和AC。
△ABC就是所求作的三角形。
討論:
1.當h>m時,兩個軌跡沒有交點,這時無解。
2.當h=m時,兩個軌跡相切,有兩個切點,這時可以作出兩個三角形,但它們是全等的。
3.當h<m時,兩個軌跡相交,有四個交點,這時可以作出四個三角形,但它們都是全等的。