基本介紹
- 中文名:跡線
- 外文名:Path Line
跡線定義
推論公式


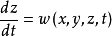
區別
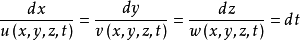




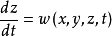
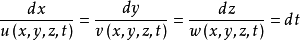

跡線是流體質點在空間運動時所描繪出來的曲線。它的切線給出同一流體質點在不同時刻的速度方向。跡線是單個質點在連續時間過程內的流動軌跡線。跡線是拉格朗日法...
A跡線是羅蘭顯示器上第一條(上方)時間基準線。羅蘭顯示器是指羅蘭導航系統的顯示器。羅蘭導航系統即LORAN,是遠程導航(long range navigation)的縮寫,是美國在二戰...
平面跡線(trace line of plane)平面上的特殊直線.平面與投影面的交線稱為平面跡線.如圖1,圖2所示.平面與V面的交線稱為正面跡線,與H面的交線稱為水平跡線...
跡線追蹤又稱“警犬追蹤”。警犬沿罪犯遺留的痕跡物品尋味搜尋,査獲犯罪分子和罪證的措施。犬對氣味的感受敏稅,分辨力強。所以可用帶有犯罪分子體味的痕跡物品,如...
星象跡線是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。...
迴轉跡線編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!中文名稱 迴轉跡線 英文名稱 turning path 定義 迴轉試驗...
在路面上行駛時,輪跡的橫向分布是不均勻的。實際上車輛輪跡僅具有一定寬度,車輛通過時只能覆蓋一小部分。因此,路面橫斷面上各個點所受到的軸載作用次數,僅為通過...
B跡線是羅蘭顯示器上第二條(下方)時間基準線。羅蘭顯示器是指羅蘭導航系統的顯示器。羅蘭導航系統即LORAN,是遠程導航(long range navigation)的縮寫,是美國在二戰...
跡線是同一流體質點在不同時刻形成的曲線,它和拉格朗日觀點相聯繫;而流線則是同一時刻不同流體質點所組成的曲線,它和歐拉觀點相聯繫。...
釋文:截層線是指被錯斷標誌面(層)在斷層面上出露的跡線。斷層兩盤同一標誌面截層線的空間關係是估算斷層相對位移(離距)的依據。1 ...
利用材料塑性變形過程中最大剪應力跡線的性質,求解塑性力學邊值問題的一種方法,主要用於求解剛塑性材料的平面應變問題。...
創建了“危石” Bayes預測模型和“危石”分布機率的跡線推測模型;推出了裂隙岩體力學空間問題等效連續隨機各向異性模型和結構面產狀參數的反演模型。主要創新成果為:...
一般旋輪線(英語:roulette),又稱為轉跡線、輪轉曲線等,是一類曲線的統稱,指一條動曲線沿一條定曲線無滑動地滾動時,動曲線上的一定點所形成的軌跡,包括擺線、...
螺旋線總偏差是指在計值範圍內,包容實際螺旋線跡線的兩條設計螺旋線之間的距離。實際螺旋線跡線用粗實線表示,設計螺旋線跡線用細點劃線表示,b 為齒寬長度,Lβ...
