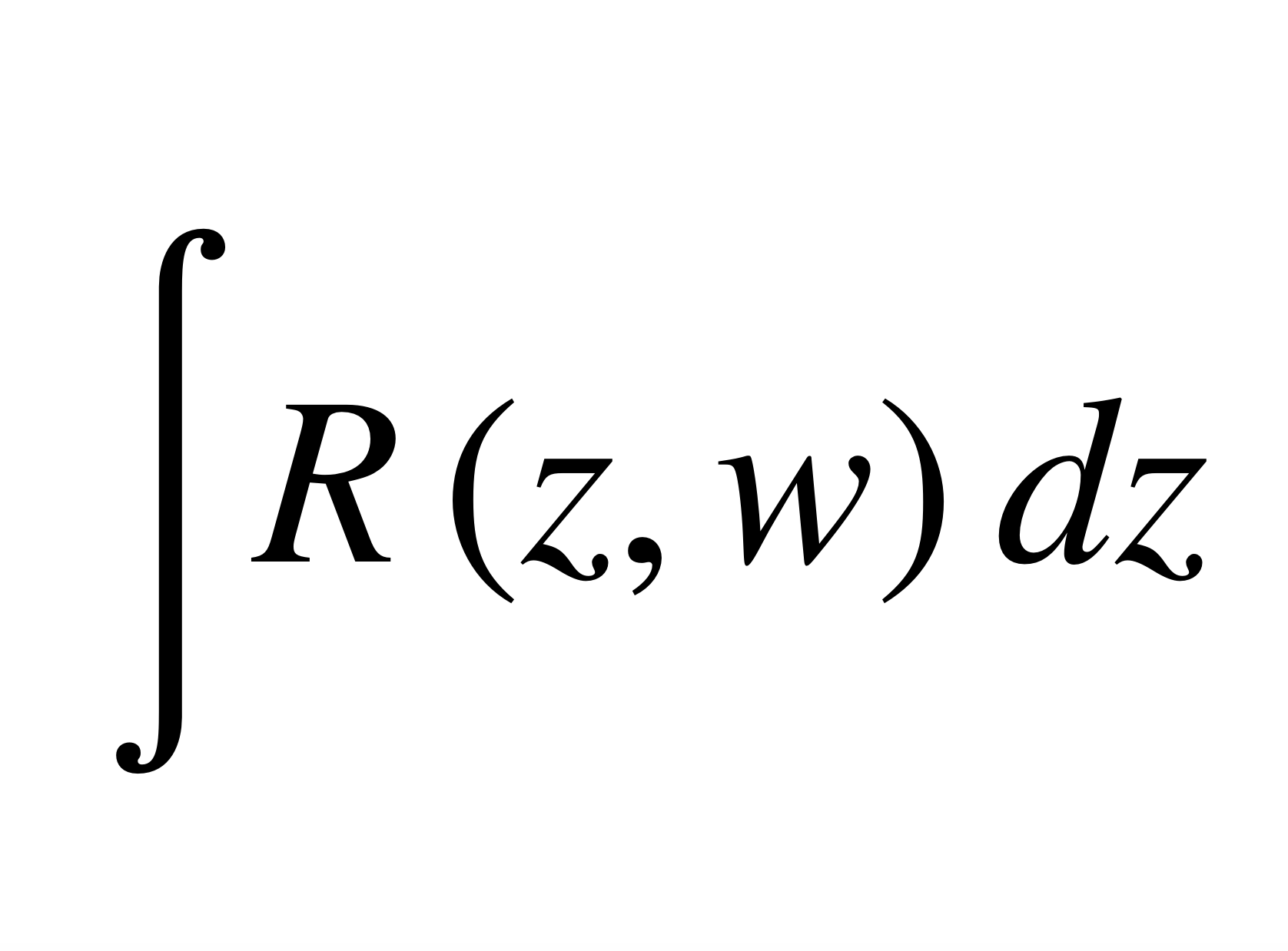超橢圓積分

簡介

超橢圓積分是一類特殊的阿貝尓積分

，其中 R 是 z，w 的有理函式(rational function)，變數z，w 滿足一個特殊類型的代數方程

。這裡 P(z) 是一個次數

的沒有重根的多項式。

當 P 的次數 m=3，4時，它是橢圓積分 (elliptic integral)，而當m=5，6時，也稱為超橢圓積分(ultra-elliptic integral) 。

方程

對應於一個虧格為 g 的雙葉緊黎曼曲面 F，其中當 m 為偶數時，g=(m-2)/2；當 m 為奇數時，g=(m-1)/2。因此對超橢圓積分有

。函式z，w ，從而

都是 F 上的單值函式。而作為定積分的積分式由 F 上的某個解析函式沿著一條可求長的路徑 L 的曲線積分(curvilinear integral) 給出，一般地其積分值完全由 L 本身的起點和終點所確定。

和阿貝尓積分的一般情形一樣，任何超橢圓積分均可表示一些初等函式和具有特殊形式的第一類、第二類、第三類典範超橢圓積分的線性組合。

因此第一類正規超橢圓積分 (normal hyper-elliptic integral of the first king) 是第一類超橢圓積分

的線性結合，這裡

對超橢圓曲面 F 的情況是第一類阿貝尓微分的最簡單的基。第二，三類阿貝尓微分及相應的超橢圓積分的顯式表達式也可以容易地算出。大體上看，超橢圓積分理論與阿貝尓積分的一般理論是一致的。

變數 z,w 的滿足方程

的所有有理函式

形成一個虧格 g 的代數函式的超橢圓域 (hyper-elliptic field)。虧格 g=1或2的緊黎曼曲面分別有一個橢圓或超橢圓域。然而當虧格 g=3 或更大時，存在結構複雜的緊黎曼曲面使得這一結論不再成立。