基本介紹
- 中文名:費曼圖
- 外文名:Feynman diagram
- 定義:第三種量子力學的方式
- 作用:廣泛運用於統計學
- 套用學科:量子力學術語
- 範疇:理工科
概念
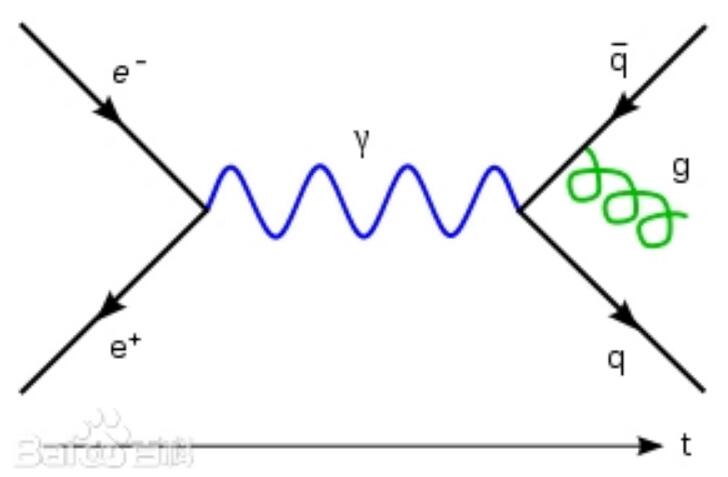
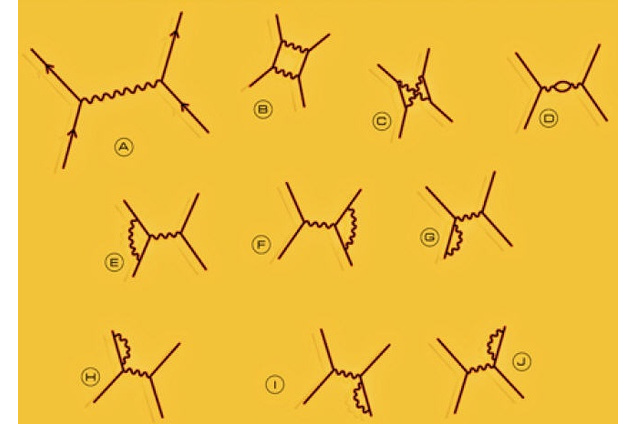
費恩曼圖一般指本詞條

《從狹義相對論到費恩曼圖》是2016年7月世界圖書出版公司出版的圖書,作者是(意)Riccardo D’Auria(R.道里亞)。內容簡介 該書填補了經典量子力學和相對量子力學及場論之間的空白。重點講述了現代理論物理學中的對稱性作用。因此該書...
《費恩曼物理學講義(第2卷)(英文版)》是一本Richard P.Feynman/Robert B.Leighton/Matthew Sands編制,由世界圖書出版公司在2004年出版的書籍。內容介紹 《費恩曼物理學講義》(第2卷)講述當時美國大學物理教學改革試圖解決的一個主要...
《你錯了·愛因斯坦先生!-牛頓·愛因斯擔·海森伯和費恩曼探討量子力學的故事》是2012年上海科技教育出版社出版的圖書,作者是哈拉爾德·弗里奇。書名 你錯了·愛因斯坦先生!-牛頓·愛因斯擔·海森伯和費恩曼探討量子力學的故事 作者 哈拉爾德...
除了這些成就之外,費恩曼博士將新的基本計算技術及記號法引時物理學,首先是無處不在的費恩曼圖,在近代科學歷史中,它比任何其他數學形式描述都更大地改變了對基本物理過程形成概念及進行計算的方法。作品目錄 第一卷 第1章 原子的運動...
《費恩曼物理學講義》由理察·費曼所著,是迄今最為經典、最為成功的物理學教材,也可以作為(高級的)科普讀物。自50年前出版以來,好評不斷。多次重新修訂。本書為系列第二卷,從普通物理水平出發,注重物理分析,深入淺出,避免運用...
費曼圖 費曼圖(Feynman Diagram)是理察·費曼提出第三種建立量子力學方式所創立的一種用形象化的方法,方便地處理量子場中各種粒子相互作用的圖。費曼規則 費曼規則(Feynman Rules)是指費曼圖與具體計算時所使用的算式之間的關係。費...
赫爾曼-費恩曼定理 赫爾曼-費恩曼定理是2019年公布的物理學名詞。 公布時間 2019年全國科學技術名詞審定委員會公審定布的物理學名詞。出處 《物理學名詞》。
費恩曼圖(英語:Feynman diagram)是美國物理學家理察·費曼(即費恩曼)在處理量子場論時提出的一種形象化的方法,描述粒子之間的相互作用、直觀地表示粒子散射、反應和轉化等過程。使用費恩曼圖可以方便地計算出一個反應過程的躍遷機率。
費恩曼圖(英語:Feynman diagram)是美國物理學家理察·費曼(即費恩曼)在處理量子場論時提出的一種形象化的方法,描述粒子之間的相互作用、直觀地表示粒子散射、反應和轉化等過程。使用費恩曼圖可以方便地計算出一個反應過程的躍遷機率。
《原子核多體理論:費恩曼圖表示與格林函式方法》的主要內容是由作者井孝功聆聽吳式樞院士講授時所做筆記整理而成的。內容簡介 格林函式方法是處理量子多體問題的有效工具,吳式樞院士生前長期致力於該方法在原子核多體理論中套用的理論...
第4章 微擾論和相互作用場 第5章 S矩陣的分振幅、費恩曼積分和費恩曼圖 第6章 重整化(一)量子電動力學單圈圖的重整化 第7章 重整化(二)重整化的BPHZ方案 第8章 BPHZ方案的收斂性 主要參考文獻 索引 封底 ...
7.4.2 費恩曼圖的解析計算 第8章 B—→K—η叼衰變的pQCD領頭階解析計算 8.1 一般情況:B(qb)→M2M3衰變 8.2 B—→K—η衰變過程的pQCD解析計算 8.3 關於pQCD次領頭階修正的討論 附錄A S矩陣,度規與Dirac矩陣 A.1 ...
