貝葉斯網路(BN),又稱為信度網,由一個有向無環圖(Directed Acylic Graph,DAG)和條件機率表(ConditionalProbability Table,CPT)組成。
基本介紹
- 中文名:貝葉斯網路模型
- 外文名:Bayesian network model
- 組成:有向無環圖、條件機率表
- 構造方式:三種
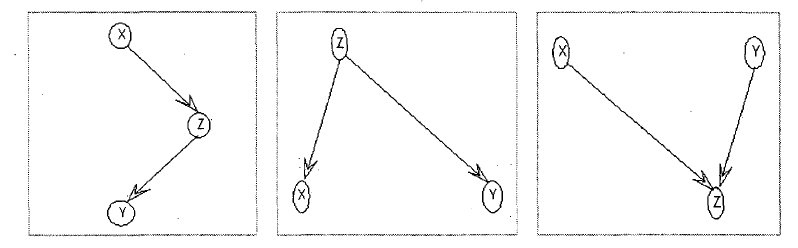
- 基本結構:順連、分連和匯連
- 又稱:信度網模型
基本結構

貝葉斯網路(BN),又稱為信度網,由一個有向無環圖(Directed Acylic Graph,DAG)和條件機率表(ConditionalProbability Table,CPT)組成。

貝葉斯網路(BN),又稱為信度網,由一個有向無環圖(Directed Acylic Graph,DAG)和條件機率表(ConditionalProbability Table,CPT)組成。...
貝葉斯網路(Bayesian network),又稱信念網路(belief network)或是有向無環圖模型(directed acyclic graphical model),是一種機率圖型模型。...
一般貝葉斯網路的構建是首先由相關領域的專家根據事物間的關係來確定出結構模型,即有向無環圖,然後再利用其它方法確定每個節點的條件機率,但這樣構建的網路模型無法...
《貝葉斯網路在智慧型信息處理中的套用》是2012年國防工業出版社出版的圖書,作者是肖秦琨、高嵩。...
《動態貝葉斯網路推理學習理論及套用》是2007年國防工業出版社出版的圖書,作者是肖秦琨,高嵩,高曉光。...
全書共13章,包括貝葉斯網路的基本理論、貝葉斯網路的結構學習、貝葉斯網路的參數學習、貝葉斯網路的推理、動態貝葉斯網路技術、貝葉斯網路的擴展模型、貝葉斯最佳化算法及...
《貝葉斯網路理論在裝備故障診斷中的套用》是2009年國防工業出版社出版的圖書,作者是李海軍。...
貝葉斯網路是基於機率推理的數學模型。採用圖形化網路結構直觀地表達變數的聯合機率分布及其條件獨立性。一個貝葉斯網路是一個有向無環圖,由代表變數節點及連線這些...
貝葉斯網路是基於貝葉斯定理的機率統計方法,是表示和處理不確定知識的理想模型。本書從限定貝葉斯網路結構規模的角度出發,對貝葉斯網路分類理論及其套用進行了深入研究,...
TAN 分類器 是由Friedman 等人提出的一種樹狀貝葉斯網路, 是樸素貝葉斯分類器的一種改進模型, TAN 分類器的分類性能明顯優於樸素貝葉斯分類器其基本思路是放鬆樸素...
BGM,意為“貝葉斯圖形模型”,由英國數學家貝葉斯在十六世紀中葉首先提出,其另一個更為人們所熟知的名稱就是套用數學的分支,統計學和機率學中常用到的“貝葉斯網路...
置信度傳播(英語:belief propagation),又稱為乘積和信息傳遞(sum-product message passing),是在貝葉斯網路、馬爾可夫隨機場等機率圖模型中用於推斷的一種信息傳遞算法...
