貝葉斯信息標準是在不完全情報下，對部分未知的狀態用主觀機率估計，然後用貝葉斯公式對發生機率進行修正，最後再利用期望值和修正機率做出最優決策，最後再利用期望值和修正機率做出最優決策，是使用的越來越多的信息指標。貝葉斯決策理論方法是統計模式識別中的一個基本方法。貝葉斯決策判據既考慮了各類參考總體出現的機率大小，又考慮了因誤判造成的損失大小，判別能力強。
基本介紹
- 中文名：貝葉斯信息標準
- 外文名：The bayesian information criteria
- 分類：計算機 自動化
- 功能：做出最優決策
- 相似詞條：貝葉斯決策依據
- 特點：信息指標
簡介,定義,基本思想,屬性,限制,套用,貝葉斯決策,理論分析,決策依據,貝葉斯網路模型,
簡介
貝葉斯信息標準是使用的越來越多的信息指標。貝葉斯信息標準有兩種不同的類型。一種貝葉斯信息標準指標用來比較所設模型與飽和模型；另一種是用來比較所設模型與零假設模型(即只包含常數項的模型)。貝葉斯信息標準是統計模型決策中的一個基本方法，其基本思想是：已知類條件機率密度參數表達式和先驗機率，利用貝葉斯公式轉換成後驗機率，根據後驗機率大小進行決策分析。
定義
貝葉斯信息標準是在不完全情報下，對部分未知的狀態用主觀機率估計，然後用貝葉斯公式對發生機率進行修正，最後再利用期望值和修正機率做出最優決策。
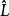
X=觀測數據
n=數據點的數量x，觀察次數或者相當於樣本量
貝葉斯信息標準是根據數據分布處於指數族的假設得出的漸近結果,用於模型選擇問題，其中向BIC添加常數不會改變結果。
基本思想
貝葉斯決策理論方法是統計模型決策中的一個基本方法，其基本思想是：
1、已知類條件機率密度參數表達式和先驗機率
2、利用貝葉斯公式轉換成後驗機率
3、根據後驗機率大小進行決策分類
屬性
1、獨立於先前或先前是“模糊”（一個常數）。
2、可以測量參數化模型在預測數據方面的效率。
3、有模型的複雜性，其中複雜性是指模型中的參數數量。
4、大致等於最小描述長度標準，但具有負號。
5、可以用於根據特定數據集中存在的固有複雜度來選擇簇數。
限制
貝葉斯信息標準主要受到兩方面的限制：
1、上述近似值僅適用於樣本大小n遠遠大於數字k的模型中的參數。
2、貝葉斯信息標準無法像高維度的變數選擇（或特徵選擇）問題那樣處理複雜的模型集合。
套用
滑坡災害是山地主要災害之一，具有分布廣泛，發生頻繁，成災快速等特點，給山區的經濟發展造成極大危害。區域滑坡空間預測主要是通過對滑坡產生條件進行分析，確定出對滑坡作用最有利的因素組合，根據這些有利的因素組合來預測區域上或某斜坡地段將來產生滑坡的可能性，圈定可能產生滑坡的影響範圍，預測可能造成的危害。單體滑坡敏感因子分析方法主要通過分析穩定性係數與抗震參數和地震強度的關係，找出敏感性最強的因素；或採用灰色關聯分析方法、正交試驗設計等方法進行敏感性因素評價。
由於一個地區歷史滑坡的發生用有或無來表示，所以可以運用區域滑坡影響因素與歷史滑坡之間建立的Logistic模型，通過貝葉斯信息標準進行模型優劣程度的比較，對影響區域滑坡的因素進行對比，得出區域滑坡敏感因子的結論，為生產實際服務。
貝葉斯決策
理論分析
1、如果我們已知被分類類別機率分布的形式和已經標記類別的訓練樣本集合，那我們就需要從訓練樣本集合中來估計機率分布的參數。在現實世界中有時會出現這種情況。（如已知為常態分配了，根據標記好類別的樣本來估計參數，常見的是極大似然率和貝葉斯參數估計方法）
2、如果我們不知道任何有關被分類類別機率分布的知識，已知已經標記類別的訓練樣本集合和判別式函式的形式，那我們就需要從訓練樣本集合中來估計判別式函式的參數。在現實世界中有時會出現這種情況。（如已知判別式函式為線性或二次的，那么就要根據訓練樣本來估計判別式的參數，常見的是線性判別式和神經網路）
3、如果我們既不知道任何有關被分類類別機率分布的知識，也不知道判別式函式的形式，只有已經標記類別的訓練樣本集合。那我們就需要從訓練樣本集合中來估計機率分布函式的參數。在現實世界中經常出現這種情況。（如首先要估計是什麼分布，再估計參數。常見的是非參數估計）
4、只有沒有標記類別的訓練樣本集合。這是經常發生的情形。我們需要對訓練樣本集合進行聚類，從而估計它們機率分布的參數。（這是無監督的學習）
5、如果我們已知被分類類別的機率分布，那么，我們不需要訓練樣本集合，利用貝葉斯決策理論就可以設計最優分類器。但是，在現實世界中從沒有出現過這種情況。這裡是貝葉斯決策理論常用的地方。
決策依據
貝葉斯決策理論方法是統計模式識別中的一個基本方法。貝葉斯決策判據既考慮了各類參考總體出現的機率大小，又考慮了因誤判造成的損失大小，判別能力強。貝葉斯方法更適用於下列場合：樣本(子樣)的數量(容量)不充分大，因而大子樣統計理論不適宜的場合；試驗具有繼承性，反映在統計學上就是要具有在試驗之前已有先驗信息的場合。用這種方法進行分類時要求兩點：
1、要決策分類的參考總體的類別數是一定的。例如兩類參考總體(正常狀態Dl和異常狀態D2)，或L類參考總體D1，D2，…，DL(如良好、滿意、可以、不滿意、不允許、……)。
2、各類參考總體的機率分布是已知的，即每一類參考總體出現的先驗機率P(Di)以及各類機率密度函式P(x/Di)是已知的。顯然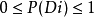
，(i=l，2，…，L)，
。
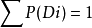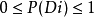
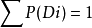
對於兩類故障診斷問題，就相當於在識別前已知正常狀態D1的機率P(D1)和異常狀態的機率P(D2)，它們是由先驗知識確定的狀態先驗機率。如果不做進一步的仔細觀測，僅依靠先驗機率去作決策，那么就應給出下列的決策規則：若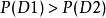
，則做出狀態屬於D1類的決策；反之，則做出狀態屬於D2類的決策。例如，某設備在365天中，有故障是少見的，無故障是經常的，有故障的機率遠小於無故障的機率。
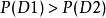
因此，若無明顯的異常狀況，就應判斷為無故障。顯然，這樣做對某一實際的待檢狀態根本達不到診斷的目的，這是由於只利用先驗機率提供的分類信息太少了。為此，還要對系統狀態進行狀態檢測，分析所觀測到的信息。
貝葉斯網路模型
貝葉斯網路是基於機率推理的數學模型。採用圖形化網路結構直觀地表達變數的聯合機率分布及其條件獨立性。一個貝葉斯網路是一個有向無環圖，由代表變數節點及連線這些節點的有向邊構成。基於貝葉斯信息標準評分的貝葉斯網路結構學習常採用如下方法：
1、基於評分一搜尋的學習方法。該方法過程簡單規範，但搜尋空間大，一般在節點有序的前提下，根據評分算法的可分解性進行局部確定或隨機搜尋(完全搜尋是NP問題)。
2、基於依賴分析的學習方法。該方法過程較複雜，但在一些假設下學習效率較高，且能獲得全局最優結構。但在現有依賴分析方法中，冗餘邊檢驗在確定邊的方向之前進行，無法準確地確定切割集，導致大量高維條件機率計算，通常不能定向所有邊。這些缺點降低了學習效率和準確性。
