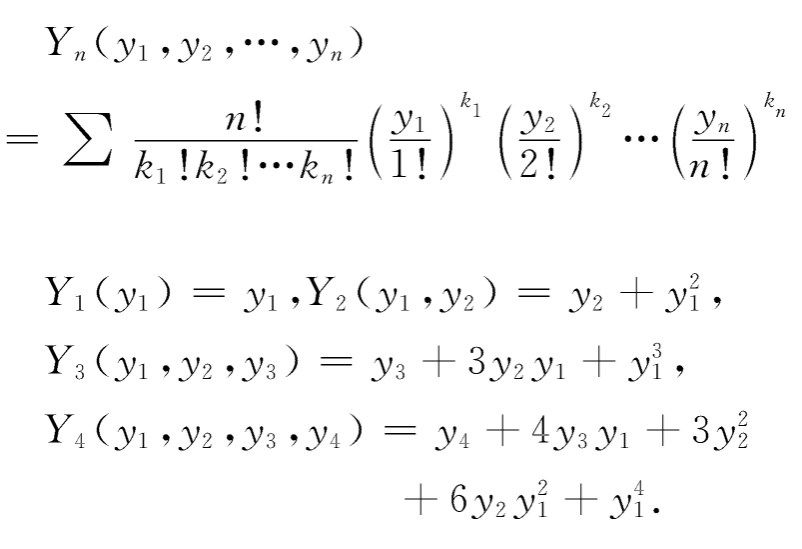貝爾多項式

貝爾多項式(Bell's polynomial)是一種組合多項式。自從美國數學家E.T.Bell在1934年的文章“Exponential Polynomials”中首次提出以來，一直是組合學界的熱門課題之一，現在 Bell多項式已經成為組合數學中的一個重要內容，在微分方程、理論物理和隨機過程中都有套用，近幾年來，Bell 多項式的恆等式及其套用引起了許多中外學者的興趣。

基本介紹

• 中文名：貝爾多項式
• 外文名：Bell's polynomial
• 所屬學科：數學（組合學）
• 簡介：一種組合多項式
• 提出者：E.T.Bell

基本介紹

貝爾多項式作為組合數學中的一個重要組合序列，在微分方程、隨機過程和理論物理中都有著重要套用，而貝爾多項式這個概念最早是由美國數學家Bell提出的，其展式如下:

這裡的和式取遍所有滿足:

的整數 ≥0。

兩類式

貝爾多項式根據其發生函式的不同分為指數型Bell多項式與普通型Bell多項式。

指數型貝爾多項式

指數型Bell多項式的實際上就是前文中所提到的Bell多項式，指數型Bell多項式是無限多變元 由雙重形式級數展開式定義的多項式(

觀察兩邊u的係數，有

其中k=0,1,2,...。

指數型貝爾多項式的顯式公式為:

和式取遍所有滿足:

的整數 ≥0。

下面是指數型Bell多項式的一些特殊值：

普通型貝爾多項式

普通型貝爾多項式是如下定義的，普通型Bell多項式是無限多變元 由雙重形式級數展開式定義的多項式A_n,k=A_n,k( )

觀察兩邊 的係數，有

其中k=0,1,2,...。

兩類貝爾多項式的關係

Port給出了兩類貝爾多項式的關係式:

由此可以得出結論，兩種貝爾多項式的恆等式是可以等價互換的。由指數型貝爾多項式的恆等式與上式，立刻可得到普通型貝爾多項式的恆等式：

廣義Bell 多項式

Comtet將Bell多項式的定義進行了推廣：設 是一列參照序列，其中 關於 的Bell多項式

定義如下:

令 ，就得到了指數型貝爾多項式；令 ，就得到普通型貝爾多項式。